Quadratwurzel

Mit der Quadratwurzel befassen wir uns in diesem Artikel. Dabei erklären wir euch, wofür man die Quadratwurzel benötigt und lieferen euch einige mathematische Gesetze sowie passende Beispiele.

Es folgt zunächst die allgemeine Darstellung eines Wurzel-Zusammenhangs sowie wichtiger Begriffe:

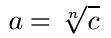
Dabei heißen "n" der Wurzelexponent, c der Radikand und a der Wurzelwert. Wurzeln mit dem Wurzelexponenten 2 heißen Quadratwurzeln. Wird bei einem Wurzelausdruck kein Wurzelexponent angegeben, ist dieser automatisch 2. Neben den Variablen a, n und c seht ihr in dieser Darstellung auch schon das Zeichen für die Wurzel.

Merke:

Quadratwurzel Beispiele

Wir haben soeben gelernt, dass Wurzeln mit dem Wurzelexponenten 2 als Quadratwurzeln bezeichnet werden. Zur besseren Verdeutlichung dazu, folgen nun zwei einfache Beispiele:

Anmerkung: In der Mathematik der Schule dürfen in der Regel keine negativen Zahlen unter der Wurzel stehen. Denn dort wird gelehrt: Aus einer negativen Zahl darf keine Wurzel gezogen werden. Der Grund dafür liegt bei der Einschränkung auf echte Zahlen. Erweitert man den Zahlenbereich auf die komplexen Zahlen, darf auch eine negative Wurzel berechnet werden.

Die Wurzelgesetze

Zur Berechnung von Wurzelausdrücken können weitere mathematische Formeln genutzt werden. Diese Formeln liefern wir euch im nun Folgenden zusammen mit entsprechenden Beispielen. Diese Regeln werden im Mathematik-Unterricht meistens als Wurzelgesetze bezeichnet.

In der Praxis müsst ihr nun erkennen, ob ihr eine der angegebenen Formeln anwenden könnt. Seht euch dazu die euch gegebene Aufgabe genau an. Liegt eine Multiplikation zweier Wurzeln vor, dann verwendet das oberste der Gesetze. Selbige Vorgehensweise gilt auch für die anderen Gesetze. Um schnell die Wurzel ziehen zu können, lernt am Besten die Gesetze auswendig. Wer dies nicht möchte, sollte eine passende Formelsammlung stets zur Hand haben.

Weitere Links:

• Zur Mathematik-Übersicht