Hypergeometrische Verteilung

Die hypergeometrische Verteilung gehört zum Bereich Stochastik / Wahrscheinlichkeitsrechnung. Was man unter einer hypergeometrischen Verteilung versteht und wie man sie berechnet, lernt ihr in diesem Artikel der Mathematik.

Starten wir zunächst kurz mit einer allgemeinen Darstellung einer hypergeometrischen Verteilung. Zum besseren Verständnis liefern wir euch im Anschluss jedoch noch ein Beispiel. Situation: In einer Urne sind N Objekte, davon haben K Objekte eine bestimmte Eigenschaft und die restlichen Objekte haben diese Eigenschaft nicht. Entnimmt man nun aus der Urne eine Stichprobe von n Objekten ohne zurücklegen, so sind die einzelnen Entnahmen nicht unabhängig. Die Zufallsgröße Y gibt die Zahl k der Objekte der Stichprobe an, welche die entsprechende Eigenschaft haben. Die Wahrscheinlichkeitsverteilung von Y nennt man hypergeometrische Verteilung "H" und berechnet sich wie folgt:

Beispiel:

In einer Urne befinden sich 10 Kugeln ( N = 10 ), davon sind 6 Kugeln rot ( K = 6 ) und 4 Kugeln weiß. Wir entnehmen 4 Kugeln ( n = 4 ) ohne zurücklegen. Wie groß ist die Wahrscheinlichkeit, dass in der Stichprobe 2 rote  Kugeln ( k = 2 ) vorhanden sind?

Lösung: Die Zahlen setzen wir in die Formel ein:

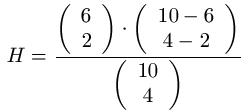
Mit dem Wissen zur Berechnung eines Binomialkoeffizienten

ergibt sich:

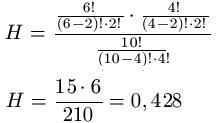
Links:

• Zur Stochastik-Übersicht
• Zurück zur Mathematik-Übersicht