Nullstellen berechnen

Um das Thema "Nullstellen berechnen" kümmern wir uns in diesem Artikel. Wir sehen uns verschiedenste Funktionen an und berechnen dann deren Nullstellen. Aber natürlich wird am Anfang erst einmal erklärt, was eine Nullstelle überhaupt ist. Dieser Artikel gehört zu unserem Bereich Mathematik.

Die Nullstelle ist ein Begriff aus dem Bereich der Mathematik, der sich mit Funktionen und ihren Verläufen und Eigenschaften befasst. Dabei versteht man unter Nullstellen die x-Werte, die eingesetzt in eine Funktion f den Funktionswert Null liefern. Wie viele Nullstellen es gibt hängt von der jeweiligen Funktion ab. Die folgenden Grafiken zeigen euch Funktionen, bei denen die Nullstelle oder die Nullstellen mit einem kleinen grünen Kreuz markiert sind.

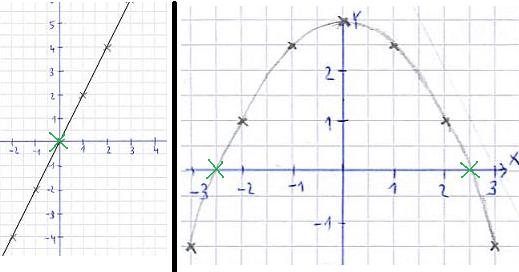
Wie viele Nullstellen eine Funktion hat - wenn sie denn überhaupt eine hat - hängt von der jeweiligen Funktion ab. Es gibt verschiedene Verfahren die Nullstellen zu berechnen, die man von der jeweiligen Funktion abhängig machen muss. Und diese sehen wir uns nun an.

Nullstelle bei linearer Funktion

Eine lineare Funktion ist eine Funktion der Form

• f(x) = y = mx + b wie zum Beispiel
• f(x) = y = 3x + 2
• f(x) = y = 7x + 6
• f(x) = y = 2x
• f(x) = y = 43x + 23

Um hier die Nullstelle zu berechnen, setzt man y = 0. Für die eben genannten Fälle wären es folgende Gleichungen, die zu lösen sind:

• 0 = 3x + 2
• 0 = 7x + 6
• 0 = 2x
• 0 = 43x + 23

Um die Berechnung der Nullstelle durchzuführen, stellt man die jeweilige Gleichung nach x um. Ausführlich wird dies im Artikel Gleichungen lösen behandelt. Soviel in Kurzform: Man formt die Gleichung so um, dass x auf einer Seite alleine steht. Für 0 = 3x + 2 erhält man dabei zunächst -2 = 3x und damit x = -2/3. Also liegt bei x = -2/3 eine Nullstelle.

Nullstelle bei quadratischen Funktionen

Um eine quadratische Gleichung wie z.B. x² + 2x + 1 = 0 nach x aufzulösen, setzen wir im nun Folgenden die PQ-Formel ein. Ich gebe euch nun erst einmal die Formel an sowie ein paar allgemeine Informationen. Keine Panik: Einige Beispiele erläutern dies im Anschluss.

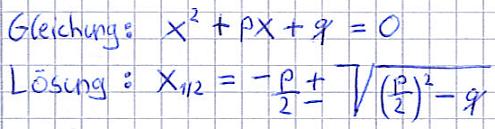
So löst man eine quadratische Gleichung:

1. Bringt die Gleichung in die Form x² + px + q = 0
2. Findet "p" und "q" raus
3. Setzt dies in die PQ-Formel ein
4. Berechnet die Formel damit

Soviel zur Theorie. Zeit dies Anhand von ein paar Beispielen zu klären. Verfolgt diese Beispiele anhand der 4-Punkte-Liste von eben.

Beispiel 1:

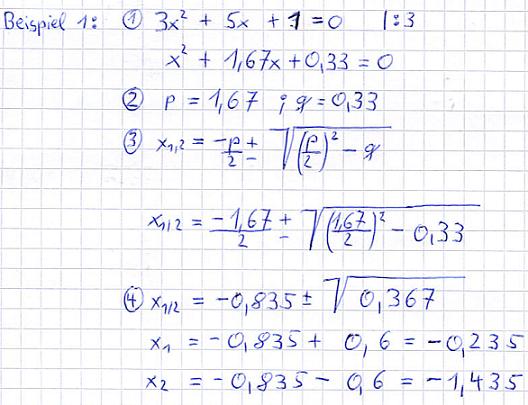
Erläuterungen: Die "3" vor dem x² stört! Dort muss immer eine "1" stehen, sprich 1x². Um dies zu erreichen, wird durch 3 dividiert. Danach wird p und q zugeordnet. Die Zahlen von p und q werden in die PQ-Gleichung eingesetzt. Danach wird der Ausdruck vor und unter der Wurzel berechnet.  Anschließend wird die Wurzel aus dem Wert gezogen und dieser wird auf das Ergebnis von vorne einmal addiert und einmal subtrahiert. Eine quadratische Gleichung hat maximal zwei Lösungen im reellen.

Beispiel 2:

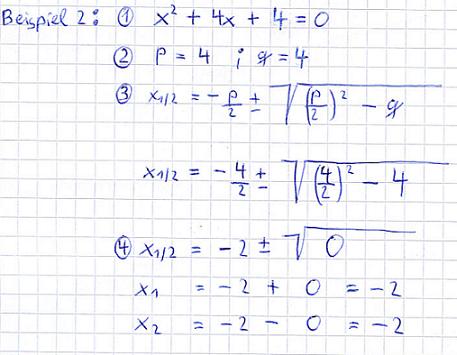
Erklärungen: Die ursprüngliche Aufgabe ist bereits in der richtigen Form. Deshalb kann p und q gleich bestimmt werden. Diese dann in die Gleichung einsetzen und ausrechnen. Wie ihr am Ergebnis seht, gibt es die Lösung -2 doppelt.

PQ Formel: Negative Wurzel / Vorzeichenbeachtung

Es gibt noch zwei kleine Hinweise bei der Berechnung von quadratischen Gleichungen mit der PQ-Formel von uns:

1. Wenn ihr die Zahlen unter der Wurzel berechnet und dann eine negative Zahl unter der Wurzel steht, dürft ihr abbrechen. Dann hat die Gleichung keine Lösung ( zumindest nicht für Schüler, Studenten müssen dann mit imaginären Rechnen ).
2. Achtet auf das Vorzeichen! Habt ihr zum Beispiel die Aufgabe x² -5x + 3 = 0 zu lösen, dann ist p=-5. Diese -5 müsst ihr dann auch in der PQ-Formel einsetzen!

Für beide Fälle findet ihr hier noch jeweils ein Beispiel:

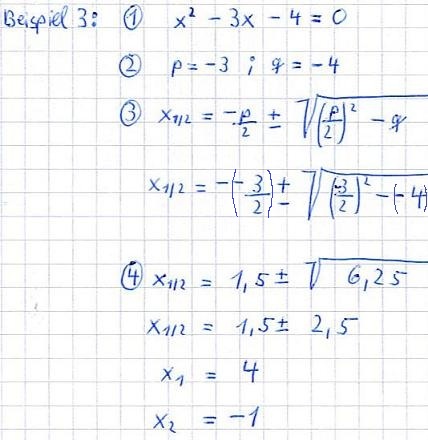
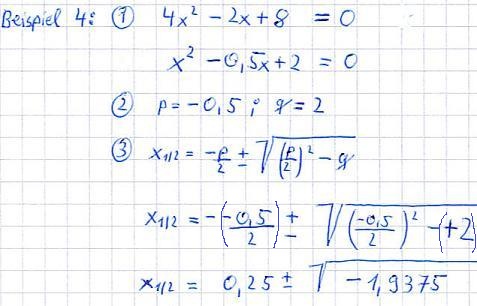
Nullstellen für Funktionen höheren Grades

Die Polynomdivision ist ein Verfahren der Mathematik, um Nullstellen von Polynomen zu berechnen. Die Berechnungsweise ähnelt der schriftlichen Division, die man bereits in der Grundschule kennen gelernt hat. Aus diesem Grund gehen wir im nun Folgenden erst einmal kurz auf die schriftliche Division ein und wenden dieses Wissen dann auf die Polynomdivision an.

Beispiel: Schriftliche Division ( Erklärung unterhalb )

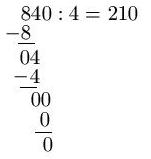
Wie funktionierte das doch gleich nochmal? Hier die Vorgehensweise:

• Ziel ist es, die Lösung der Aufgabe 840 : 4 zu finden
• Die erste Zahl ist die 8. Teilt man 8 : 4 erhält man eine 2. Dies ist die erste Zahl für die Lösung
• Jetzt wieder zurück gerechnet: 2 · 4 = 8. Diese 8 wird unter die erste 8 am Anfang geschrieben.
• Jetzt werden die beiden Zahlen voneinander abgezogen, deshalb das "-" vor der unteren Zahl. 8 - 8 ergibt 0.
• Jetzt wird die nächste Zahl von oben runter geholt: Das ist eine 4.
• Jetzt wird wieder geteilt. 4 : 4 = 1. Die 1 wird wieder hingeschrieben
• Rückrechnen: 1 · 4 = 4. Die 4 wird wieder unter die andere 4 geschrieben
• Jetzt wird wieder abgezogen: 4 - 4 = 0.
• Die Null wird hingeschrieben. Von oben wird die nächste Zahl auch runter gezogen, ebenfalls eine 0.
• 0 : 4 = 0. Eine Null wird an das Ergebnis angehängt.
• Rückrechnung: 0 · 0 = 0 und 0 - 0 bleibt Null. Es gibt keine weitere Zahl von oben zu holen
• Es sind nur noch Nullen übrig. Damit ist dir Rechnung fertig.

Polynomdivision Erklärung ( Nullstellen berechnen )

Bei der Polynomdivision dividiert man nun nicht zwei Zahlen, sondern ganze Terme. In der Mathematik bezeichnet der Begriff Term einen sinnvollen Ausdruck, der Zahlen, Variablen, Symbole ( für mathematische Verknüpfungen ) und Klammern enthalten kann. Um eine Polynomdivision durchzuführen, benötigt man einen Term und eine Nullstelle dieses Terms.

Diese Nullstelle zu finden, ist oft recht schwierig. In der Schule gibt der Lehrer bzw. die Lehrerin die Nullstelle in aller Regel vor. Ist dies nicht der Fall, kann eine Nullstelle durch Raten oder numerische Verfahren gefunden werden. Für die nun folgenden Beispiele, gehen wir davon aus, dass eine Nullstelle bereits gegeben ist.

Polynomdivision Beispiel 1:

Gegeben sei die Funktion y = f(x) = x³ - 2x² - 5x + 6. Durch probieren wurde eine Nullstellen bei x = 1 gefunden. Es soll nun die Polynomdivision durchgeführt werden, um im Anschluss alle Nullstellen zu finden.

Lösung: Wir dividieren die Funktion y = f(x) durch ( x - 1 ). Dies sieht wie folgt aus:

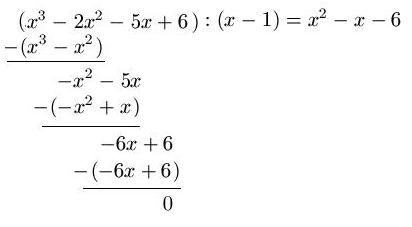
Wir dividieren hier zunächst x³ : x = x². Im Anschluss multiplizieren wird x² · ( x - 1 ) = x³ - x². Anschließend wird ( x³ - 2x² ) - ( x³ - x² ) berechnet. Danach beginnt das Spiel wieder von vorne, bis die Division komplett ist. Die Vorgehensweise entspricht der schriftlichen Division. Das Ergebnis der Polynomdivision lautet x² - x - 6. Ob das Ergebnis stimmt, erfahren wir durch eine Probe:

Probe: ( x² - x - 6 ) · ( x - 1 ) = x³ - 2x² -5x + 6  // Die Lösung stimmt

Um nun noch die restlichen Nullstellen zu berechnen, wenden wir die PQ-Formel auf x² - x - 6 an und erhalten x₂ = 3 und x₃ = -2. Wir wissen somit, dass bei 1, 3 und -2 die Nullstellen liegen ( also wenn wir diese Zahlen für x einsetzen ). Das Polynom kann man somit in seine Linearfaktoren zerfallen lassen. f(x) = ( x - 1 ) ( x - 3 ) ( x + 2 ). Auch hier führen wir die Probe durch:

Probe: ( x - 1 ) ( x - 3 )  ( x + 2 ) = x³ - 2x² - 5x + 6 // Die Lösung stimmt

Polynomdivision Beispiel 2

Gegeben sei die Funktion y = f(x) = 3x³ - 10x² + 7x - 12. Eine Nullstelle bei x = 3 sei bekannt. Gesucht sind alle Nullstellen von f(x).

Lösung: Wie dividieren zunächst die Funktion f(x) durch ( x - 3 ). Dies sieht wie folgt aus:

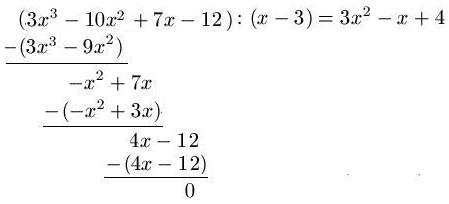
Auch hier berechnen wir Stück für Stück das Ergebnis. Zunächst wird 3x³ : ( x - 3 ) berechnet, das Ergebnis lautet 3x². Wir multiplizieren zurück: 3x² · ( x - 3 ) und erhalten 3x³ - 9x². Dann subtrahieren wir wieder. Das Ergebnis der Polynomdivision lautet 3x² - x + 4. Wir führen eine Probe zur Sicherheit durch.

Probe: ( x - 3 ) ( 3x² -x + 4 ) = 3x³ - 10x² + 7x - 12

Um weitere Nullstellen zu berechnen, wenden wir auf die 3x² - x + 4 = 0 die PQ Formel an. Bei der Anwendung der PQ-Formel erhält man eine negative Zahl unter der Wurzel. Damit endet die Rechnung ( für Schüler ) und die einzige Nullstelle liegt bei x = 3.

Links:

• Zur Ableitung-Übersicht
• Zur Mathematik-Übersicht