Zahlengerade ▷ Erklärung und Beispiele

Die Zahlengerade mit vielen Beispielen sehen wir uns hier an. Du bekommst eine Definition zur Zahlengerade und erfährst, welche Zahlen darauf eingetragen werden. Dazu werden Beispiele mit ganzen Zahlen, rationalen Zahlen bzw. Brüchen und Dezimalzahlen vorgestellt. Die Inhalte liegen als Text und als Video vor.

Eine Zahlengerade ist eine Linie, auf der Zahlen in gleichen Abständen eingetragen werden. Im Gegensatz zum Zahlenstrahl kann eine Zahlengerade nicht nur positive Zahlen, sondern auch negative Zahlen aufweisen. Ein leerer Zahlenstrahl kann zum Beispiel so dargestellt werden:

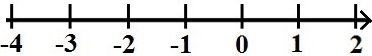
Im einfachsten Fall werden auf der Zahlengerade ganze Zahlen dargestellt. Darunter fallen die positiven ganzen Zahlen (1, 2, 3, 4 und so weiter) und die negativen ganzen Zahlen (-1, -2, -3, -4 und so weiter) sowie die Null (0).

Die Zahlengerade kann jedoch auch für rationale Zahlen bzw. Brüche und Dezimalzahlen verwendet werden. Dazu mehr im nächsten Abschnitt.

Zahlengerade: rationale Zahlen (Brüche) und Dezimalzahlen

Auf einer Zahlengerade können auch rationale Zahlen dargestellt. Rationale Zahlen sind Zahlen, die in Form von einem Bruch dargestellt werden können. Als Beispiel wird der Bereich zwischen -1 und +1 auf der Zahlengerade vergrößert und erneut unterteilt. Für diese Zahlengerade wurde der Bereich zwischen zwei ganzen Zahlen in 4 gleich große Abschnitte unterteilt. Dies sieht du am Nenner 4.

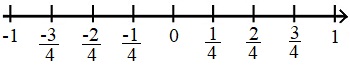
Neben Brüchen können auch Dezimalzahlen (Kommazahlen) auf einer Zahlengerade dargestellt werden. Bei der nächsten Zahlengerade wurden erneut die Bereiche zwischen zwei ganzen Zahlen in 4 gleich große Abschnitte unterteilt. Die Brüche aus dem letzten Beispiel wurden dazu in Dezimalzahlen umgewandelt.

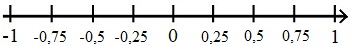
Die Zahlengerade wird in der Schule dazu verwendet das Rechnen mit negativen Zahlen zu verstehen. Eine Einführung zur Addition und Subtraktion und die Mitte zwischen zwei Zahlen sehen wir uns in den nächsten Abschnitten an.

Rechnen mit der Zahlengerade

Die Grundrechenarten Addition und Subtraktion mit negativen Zahlen können sehr einfach mit der Zahlengerade erklärt werden. Eine Addition bedeutet auf der Zahlengerade nach rechts zu gehen. Im nächsten Beispiel geht es von der negativen Zahl -3 um 4 nach rechts auf die positive Zahl +1.

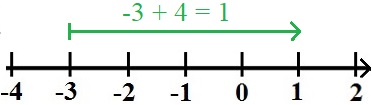
Eine Subtraktion bedeutet auf der Zahlengerade nach links zu gehen. Im nächsten Beispiel wird von der positiven Zahl +1 um 4 nach links gegangen. Die Differenz - sprich das Ergebnis der Subtraktion - ist die -3.

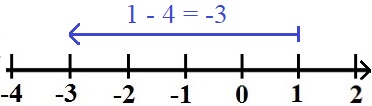
Ein sehr wichtiger Zusammenhang zwischen Zahlen lässt sich ebenfalls sehr einfach mit der Zahlengerade verstehen. Die nächste Zahlengerade zeigt, dass der Abstand von der -2 zur 0 genau so groß ist wie der Abstand von +2 zur 0.

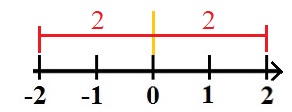
In der Mathematik wird dies wie folgt formuliert: Der Betrag der Zahl -2 und auch der Betrag der Zahl +2 sind jeweils +2, denn der Abstand zur 0 ist jeweils 2.

Die Mitte zwischen zwei Zahlen

Die Mitte zwischen zwei Zahlen lässt sich ebenfalls mit der Zahlengerade verdeutlichen. Aufgabe: Wo liegt die Mitte zwischen den Zahlen -43 und +29? Um dieses Problem zu verstehen, machen wir uns zunächst eine Skizze mit den Zahlen -43, +29 und 0.

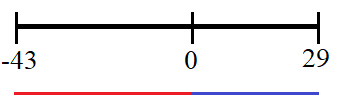
Von der -43 bis zur 0 ist der Abstand 43. Von der 0 bis zur 29 ist der Abstand 29. Der Gesamtabstand zwischen den beiden Zahlen ist damit 43 + 29 = 72. Der halbe Abstand (Mitte) ist die Hälfte von 72, daher 36.

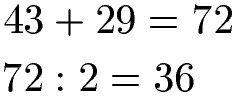
Die gesuchte Zahl liegt damit um 36 nach rechts gesehen von der -43 oder um 36 nach links gesehen von der +29. Um die Zahl in der Mitte zu finden, müssen wir daher auf die Ausgangszahlen entweder 36 addieren oder subtrahieren:

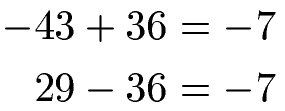
Die Mitte zwischen -43 und +29 liegt damit bei -7.