Das Bruchrechnen lernst du in diesem Artikel mit vielen Beispielen. Du erfährst außerdem wie das Rechnen mit Brüchen (Addition, Subtraktion, Multiplikation und Division) funktioniert. Das Erweitern und Kürzen von Brüchen sowie gemischte Zahlen werden ebenfalls ganz einfach erklärt. Die Inhalte liegen als Text und Video vor.
Brüche dienen dazu Anteile an etwas Ganzem darzustellen. So kann es passieren, dass nur ein Teil einer Pizza gegessen wird und nur ein Teil einer Flasche getrunken wird. In der Mathematik werden solche Teile mit einem Bruch dargestellt. Die nächste Grafik zeigt wie 3 von 7 Kästchen gelb markiert werden und wie der entsprechende Bruch dargestellt wird.
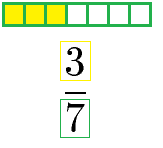
Ein Bruch besteht aus einem Zähler, einem Bruchstrich und einem Nenner. Der Zähler steht über dem Bruchstrich, der Nenner steht unter dem Bruchstrich.

Merke dir unbedingt wo sich Zähler und Nenner bei einem Bruch befinden.
Bruchrechnen Regel 1: Zähler und Nenner
Dies solltest du dir zu den Begriffen der Bruchrechnung merken:
- Der Nenner gibt die Anzahl aller Teile an.
- Der Zähler gibt die Anzahl der ausgewählten Teile an.
- Der Bruchstrich trennt Zähler und Nenner.
Brüche werden ab der 5. Klasse oder spätestens ab der 6. Klasse in der Schule behandelt. Sobald die Grundlagen zu Brüchen geklärt sind wird mit Bruchrechnung begonnen. Diese sehen wir uns nun ebenfalls an.
Bruchrechnen: Brüche addieren und subtrahieren
Brüche mit gleichen Nennern (= gleichnamige Brüche) werden addiert indem die Zähler addiert werden und der Nenner beibehalten wird. So werden aus 2 von 6 Stücken plus 3 von 6 Stücken insgesamt 5 von 6 Stücken.
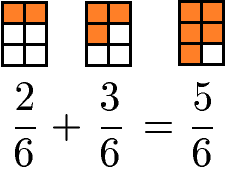
Zur Subtraktion gleichnamiger Brüche werden die Zähler subtrahiert und der Nenner beibehalten. Werden bei 5 von 6 Stücke nun 3 von 6 Stücke weggenommen, bleiben 2 der 6 Stücke übrig.
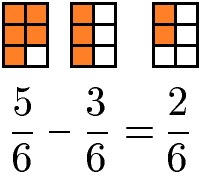
Bruchrechnen Regel 2: Addition und Subtraktion gleichnamiger Brüche
Brüche mit gleichen Nennern werden addiert oder subtrahiert indem die Zähler addiert oder subtrahiert werden und der Nenner beibehalten wird.
Bruchrechnung für ungleichnamige Brüche
Um Brüche mit verschiedenen Nennern (= ungleichnamige Brüche) zu addieren oder zu subtrahieren, müssen die Brüche zunächst gleichnamig gemacht werden. Darunter versteht man die Brüche so umzuformen, dass nur gleichnamige Brüche entstehen. Achte im nächsten Beispiel darauf wie die Streifen in 3 oder 4 Teile zerlegt werden. Die Streifen beim linken Bruch sind dabei größer als beim rechten Bruch.
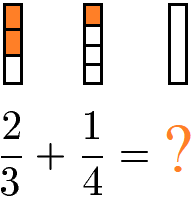
Um die Brüche gleichnamig zu machen muss ein gemeinsamer Nenner gefunden werden. Die einfachste Erklärung besteht darin zunächst die beiden Nenner miteinander zu multiplizieren.
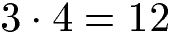
Die Zahl 12 stellt einen gemeinsamen Nenner für beide Brüche dar. Mit anderen Worten: Wir müssen beide Brüche auf die Zahl 12 im Nenner umrechnen. Um dies zu erreichen, wird der erste Bruch mit 4 erweitert und der zweite Bruch wird mit 3 erweitert. Erweitern bedeutet den Zähler und den Nenner mit der gleichen Zahl zu multiplizieren. Im Anschluss können die beiden gleichnamigen Brüche addiert werden.
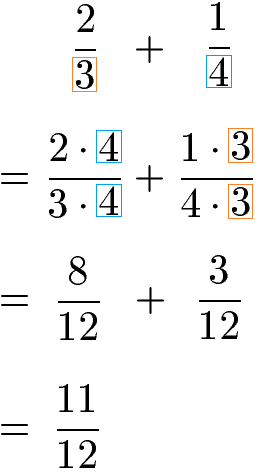
Weitere Erklärungen und Beispiele findest du unter Brüche addieren und Brüche subtrahieren.
Bruchrechnen Regel 3: Ungleichnamige Brüche addieren oder subtrahieren
Um Brüche mit verschiedenen Nennern (= ungleichnamige Brüche) zu addieren oder zu subtrahieren, müssen alle Brüche zunächst auf einen gemeinsamen Nenner gebracht werden.
Das Erweitern und Kürzen von Brüchen sehen wir uns weiter unten noch einmal genauer an. Zunächst kommen wir jedoch zur Multiplikation oder Division von Brüchen.
Brüche multiplizieren und dividieren
Brüche werden multipliziert indem die Zähler und Nenner jeweils miteinander multipliziert werden: Zähler mal Zähler und Nenner mal Nenner. Beim Bruchrechnen mit der Grundrechenart Multiplikation spielt es keine Rolle, ob die die Nenner gleich oder verschieden sind.
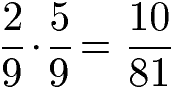
Bei der Multiplikation von Brüchen mit unterschiedlichen Nennern (= ungleichnamige Brüche) werden ebenfalls die Zähler und Nenner jeweils miteinander multipliziert. Im Unterschied zur Addition müssen die Brüche demnach nicht auf einen gemeinsamen Nenner gebracht werden.
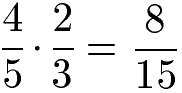
Bruchrechnen Regel 4: Brüche multiplizieren
Um Brüche zu multiplizieren wird Zähler mit Zähler und Nenner mit Nenner multipliziert.
Die Division von Brüchen basiert auf der Multiplikation von Brüchen. Um zwei Brüche zu dividieren, wird aus der Geteiltaufgabe eine Malaufgabe gemacht. Dazu wird das Geteiltzeichen durch ein Malzeichen ersetzt. Um dies tun zu dürfen wird beim zweiten Bruch Zähler und Nenner vertauscht.
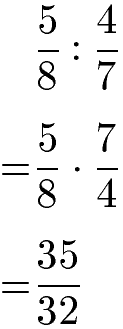
Weitere Beispiele und Erklärungen findest du unter Brüche multiplizieren und Brüche dividieren.
Bruchrechnen Regel 5: Brüche dividieren
Um Brüche zu dividieren, wird die Division in eine Multiplikation umgewandelt. Das Geteiltzeichen wird durch ein Malzeichen ersetzt. Dafür müssen beim zweiten Bruch Zähler und Nenner vertauscht werden. Im Anschluss werden die beiden Brüche multipliziert.
Wir kennen nun alle Grundrechenarten zur Bruchrechnung: Addition, Subtraktion, Multiplikation und Division. Sehr wichtig für das Bruchrechnen ist es jedoch ebenfalls Brüche kürzen und erweitern zu können. Dies sehen wir uns als nächstes an.
Brüche erweitern und kürzen
Werden Brüche im Zähler und im Nenner mit der gleichen Zahl multipliziert wird diese in der Bruchrechnung als "Bruch erweitern" bezeichnet. Beim Erweitern von Brüchen ändert sich der Wert des Bruches nicht. In der nächsten Grafik ist stets die halbe Fläche gelb markiert, egal aus wie vielen Teilen diese besteht.
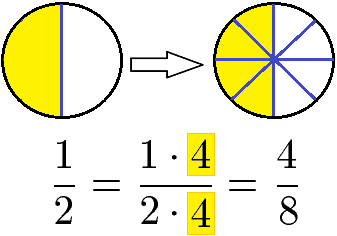
Das Erweitern von Brüchen bedeutet den Zähler und den Nenner mit der gleichen Zahl zu multiplizieren. Im nächsten Beispiel wird der Bruch mit der Zahl 2 erweitert.

Bruchrechnen Regel 6: Brüche erweitern
Brüche zu erweitern bedeutet den Zähler und den Nenner mit der gleichen Zahl zu multiplizieren.
Werden Brüche im Zähler und im Nenner durch die gleiche Zahl dividiert wird diese in der Bruchrechnung als "Bruch kürzen" bezeichnet. Beim Kürzen von Brüchen ändert sich der Wert des Bruches nicht. In der nächsten Grafik ist stets die halbe Fläche gelb markiert, egal aus wie vielen Teilen diese besteht.
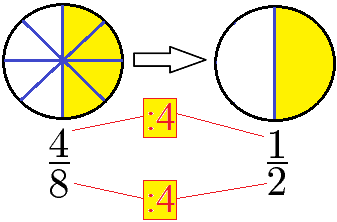
Das Kürzen von Brüchen bedeutet den Zähler und den Nenner durch die gleichen Zahl zu teilen. Im nächsten Beispiel wird der Bruch mit der Zahl 10 gekürzt.
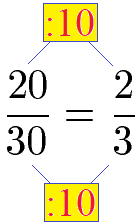
Weitere Erklärungen und Beispiele findest du unter Brüche kürzen und Brüche erweitern.
Bruchrechnen Regel 7: Brüche kürzen
Brüche zu kürzen bedeutet den Zähler und den Nenner durch die gleiche Zahl zu dividieren.
Bruchrechnung: Gemischte Zahlen und gemischte Brüche
In der Bruchrechnung existieren gemischte Zahlen bzw. gemischte Brüche. Eine gemischte Zahl bzw. ein gemischter Bruch besteht aus einer ganzen Zahlen und einem Bruch. Die nächste Grafik zeigt 2 ganze Pizzen und von einer dritten Pizza noch 3 von 4 Stücken. Dies sind damit 2 Ganze und 3 von 4 Stücken.
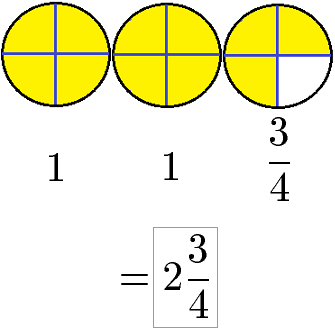
Um mit gemischten Brüchen rechnen zu können, müssen diese in gewöhnliche Brüche aus nur Zähler und Nenner umgerechnet werden. Als Beispiel dient uns die Multiplikation zweier gemischter Zahlen.
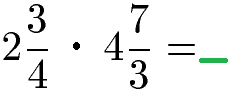
Im ersten Schritt werden beide gemischte Zahlen in Brüche aus nur Zähler und Nenner umgewandelt. Dazu wird die ganze Zahl mit dem Nenner des Bruchs erweitert. Der Nenner des ersten Bruches ist hier 4, daher wird die ganze Zahl mit 4 erweitert, sprich Zähler und Nenner mit dieser Zahl multipliziert. Danach können die gleichnamigen Brüche addiert werden.
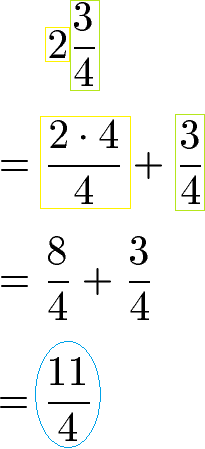
Der zweite gemischte Bruch muss ebenfalls umgewandelt werden. Die ganze Zahl 4 wird daher mit dem Nenner (3) erweitert, sprich wir multiplizieren die 4 mit 3 und teilen durch 3. Dadurch erhalten wir zwei gleichnamige Brüche für die Addition.
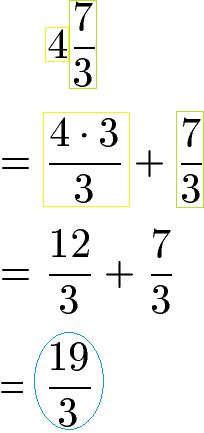
Beide gemischte Zahlen wurden nun in unechte Brüche umgewandelt. Unecht sind die Brüche da beide Brüche einen größeren Zähler als Nenner haben. Die beiden nun umgewandelten Brüche können jetzt sehr einfach multipliziert werden: Zähler mal Zähler und Nenner mal Nenner.
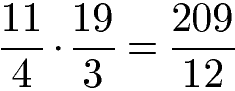
Bruchrechnen Regel 8: Gemischte Brüche
Vor dem Rechnen mit gemischten Brüche sollten diese in gewöhnliche Brüche mit nur Zähler und Nenner umgewandelt werden. Dazu wird die ganze Zahl mit dem Nenner erweitert und die gleichnamigen Brüche addiert.
Im nächsten Abschnitt sehen wir uns noch eine Zusammenfassung der Regeln zum Bruchrechnen an sowie weiterführende Themen.
Bruchrechnen Regeln: Zusammenfassung
Wichtiges Wissen und Regeln zum Bruchrechnen in der Zusammenfassung:
- Regel 1 (Begriffe): Der Zähler steht beim Bruch oben, der Nenner steht unten. Der Nenner gibt die Anzahl aller Teile an. Der Zähler gibt die Anzahl der ausgewählten Teile an.
- Regel 2 (Gleichnamige Brüche): Brüche mit gleichen Nennern werden addiert oder subtrahiert indem die Zähler addiert oder subtrahiert werden und der Nenner beibehalten wird.
- Regel 3 (Ungleichnamige Brüche): Um Brüche mit verschiedenen Nennern (= ungleichnamige Brüche) zu addieren oder zu subtrahieren, müssen alle Brüche zunächst auf einen gemeinsamen Nenner gebracht werden.
- Regel 4 (Brüche multiplizieren): Um Brüche zu multiplizieren wird Zähler mit Zähler und Nenner mit Nenner multipliziert.
- Regel 5 (Brüche dividieren): Um Brüche zu dividieren wird die Division in eine Multiplikation umgewandelt. Das Geteiltzeichen wird durch ein Malzeichen ersetzt. Dafür müssen beim zweiten Bruch Zähler und Nenner vertauscht werden. Im Anschluss werden die beiden Brüche multipliziert.
- Regel 6 (Brüche erweitern): Brüche zu erweitern bedeutet den Zähler und den Nenner mit der gleichen Zahl zu multiplizieren.
- Regel 7 (Brüche kürzen): Brüche zu kürzen bedeutet den Zähler und den Nenner durch die gleiche Zahl zu dividieren.
- Regel 8 (Gemischte Brüche): Vor dem Rechnen mit gemischten Brüchen sollten diese in gewöhnliche Brüche mit nur Zähler und Nenner umgewandelt werden. Dazu wird die ganze Zahl mit dem Nenner erweitert und die gleichnamigen Brüche addiert.
Dies war eine durchaus ausführliche Einführung in die Bruchrechnung. Möchtest du dir die eben angesprochenen Themen noch ausführlicher ansehen findest du zu allen Themen in der nächsten Liste mit weiteren Erklärungen.
Mehr zur Bruchrechnung:
- Brüche addieren
- Brüche subtrahieren
- Brüche multiplizieren
- Brüche dividieren
- Brüche kürzen
- Brüche erweitern
- Kehrwert
- Hauptnenner
- Gemischte Zahlen / Gemischte Brüche
- Doppelbruch / Mehrfachbruch/ Mehrere Brüche
- Bruchterme
- Übungsaufgaben mit Lösungen
- Bruchrechnung: Einführung und Regeln
- Bruch in Dezimalzahlen
Weitere Themen: Zähler, Bruchstrich, Nenner, Unechter Bruch, Gemeine Brüche, Echter Bruch, Gleichnamige Brüche, Ungleichnamige Brüche, Dezimalbruch, Unechter Dezimalbruch, Endlicher Dezimalbruch, Periodische Dezimalbrüche, Echter Dezimalbruch
Links:
1832 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige: