Rationale Zahlen werden in diesem Artikel mit vielen Beispielen erklärt. Mit einer Tabelle verstehst du den Unterschied zwischen rationalen Zahlen und nicht rationalen Zahlen. Wichtige Eigenschaften zu dieser Zahlenart und das Rechnen mit rationalen Zahlen (Brüche und Dezimalzahlen) zeige ich dir ebenfalls. Die Inhalte liegen als Text und als Video vor.
Beginnen wir mit einer einfachen Definition zu rationalen Zahlen: Eine rationale Zahl ist eine Zahl, die als Bruch aus ganzen Zahlen dargestellt werden kann. Zu den rationalen Zahlen gehören:
- Alle natürlichen Zahlen (1, 2, 3, 4, ...).
- Alle ganzen Zahlen (... -3, -2, -1, 0, 1, 2, 3, ...).
- Brüche mit ganzen Zahlen im Zähler und Nenner.
- Endliche Dezimalzahlen (Kommazahlen).
- Dezimalzahlen mit periodischen Ziffern nach dem Komma.
Die nächste Tabelle zeigt einen Vergleich zwischen natürlichen und ganzen Zahlen sowie rationalen und irrationalen Zahlen (= nicht rationale Zahlen).
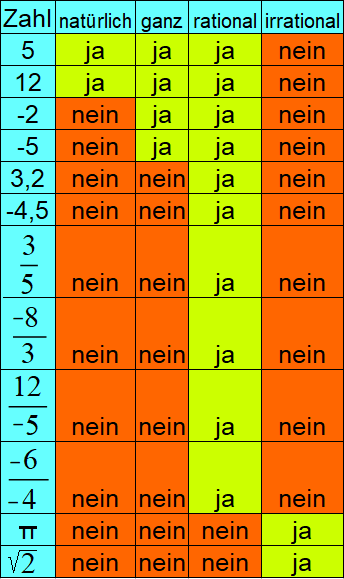
Nicht rationale Zahlen (= irrationale Zahlen) sind Zahlen mit unendlich vielen Stellen nach dem Komma, die jedoch nicht periodisch sind. Weitere Erklärungen und Beispiele zu rationalen und irrationalen Zahlen sehen wir uns gleich an. Fasst man rationale Zahlen und irrationale Zahlen zusammen erhält man die reellen Zahlen.
Rationale Zahlen: Brüche und Dezimalzahlen
Rationale Zahlen können in Form von Brüchen oder als Dezimalzahlen dargestellt werden. Die Darstellung in Brüchen erfolgt mit ganzen Zahlen in Zähler und Nenner oder kann durch Umrechnung auf diese Darstellung gebracht werden. Hinweis: In der Mathematik darf nicht durch die Zahl 0 (Null) geteilt werden. Daher darf in einem Bruch der Nenner nicht 0 sein.
Sowohl positive als auch negative Zahlen können in Zähler und Nenner vorkommen. Die nächsten Brüche sind rationale Zahlen.
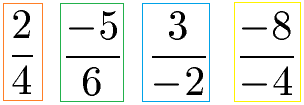
Brüche können ausgerechnet werden (Siehe Bruch in Dezimalzahlen umwandeln). Beim Ausrechnen eines Bruchs entsteht meistens eine Dezimalzahl, umgangssprachlich auch Kommazahl genannt. In manchen Fällen entsteht auch eine natürliche oder ganze Zahl. Die nächsten vier Zahlen sind Beispiele für rationale Zahlen:

Das Symbol oder Zeichen für rationale Zahlen ist ein Q mit doppeltem Strich in den meisten Bereichen:
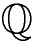
Rationale Zahlen können mit dem Symbol Q und geschweiften Klammern in eine Menge geschrieben werden:
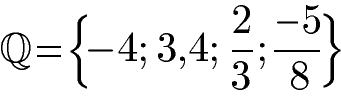
Im Vergleich zu rationalen Zahlen gibt es irrationale Zahlen. Unter irrationalen Zahlen versteht man Dezimalzahlen (Kommazahlen) mit unendlich vielen Stellen nach dem Komma. Diese Stellen nach dem Komma sind jedoch nicht periodisch, sprich es gibt keine Wiederholung bestimmter Ziffern nach dem Komma. Beispiele für irrationale Zahlen sind die Wurzel aus 2, die Kreiszahl Pi oder die eulersche Zahl.

Rationale Zahlen am Zahlenstrahl (Zahlengerade)
Rationale Zahlen können auf einem Zahlenstrahl oder einer Zahlengerade dargestellt werden. Zur Erinnerung: Auf einem Zahlenstrahl befinden sich nur positive Zahlen. Eine Zahlengerade umfasst positive und negative Zahlen.
Rationale Zahlen Dezimalzahlen:
Die nächste Grafik zeigt rationale Zahlen in Form von Dezimalzahlen (Kommazahlen) auf einer Zahlengerade. Die Darstellung in Form von Dezimalzahlen erlaubt es auf einfache Art und Weise auch Dezimalzahlen zwischen zwei Strichen einzutragen. Die -0,25 in blau befindet sich direkt auf einem Strich mit Zahl. Alle anderen rationalen Zahlen werden jedoch zwischen den Strichen für die Einteilung eingetragen.
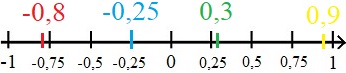
Ein Zahlenstrahl oder eine Zahlengerade hilft dabei Zahlen der Größe nach zu vergleichen. Je weiter links eine Zahl auf dem Zahlenstrahl oder der Zahlengerade steht, desto kleiner ist die Zahl. Negative Zahlen sind daher immer kleiner als positive Zahlen. Die nächsten rationalen Zahlen sind von klein nach groß geordnet, wobei die kleinste Zahl ganz links steht.
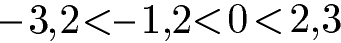
Rationale Zahlen Brüche:
Rationale Zahlen können auch in Form von Brüchen auf einem Zahlenstrahl oder einer Zahlengerade eingetragen werden. Im Gegensatz zu Dezimalzahlen ist es jedoch sehr schwierig Brüche zu markieren die nicht direkt auf den Strichen der Einteilung liegen. Solltest du dies müssen, empfehle ich dir, den Zahlenstrahl oder die Zahlengerade noch feiner einzuteilen.
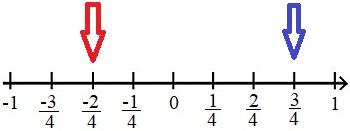
Rationale Zahlen in Form von Brüchen können ebenfalls verglichen und sortiert werden. Wie auch bei Dezimalzahlen sind Brüche mit negativem Vorzeichen kleiner als Brüche mit positivem Vorzeichen. Je weiter rechts ein Bruch auf dem Zahlenstrahl vorkommt, desto größer ist der Bruch.
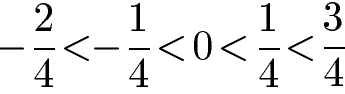
Sehen wir uns nun das Rechnen mit rationalen Zahlen und die Rechengesetze an.
Rechnen mit rationalen Zahlen
Ab der 5. Klasse oder spätestens ab der 6. Klasse wird in Mathematik mit rationalen Zahlen gerechnet. Alle Grundrechenarten werden ab dann mit Dezimalzahlen oder Brüchen durchgeführt.
Rationale Zahlen addieren:
Rationale Zahlen in Form von Dezimalzahlen bzw. Kommazahlen werden addiert, indem die Zahlen untereinander geschrieben werden. Dabei steht Komma unter Komma. Für die Berechnung wird die schriftliche Addition verwendet.
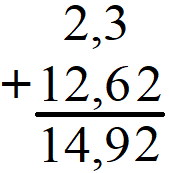
Weitere Erklärungen und (schwierigere) Beispiele findest du unter Rechnen mit Dezimalzahlen. Die Addition von rationalen Zahlen als Brüche wird mit den Regeln der Bruchrechnung durchgeführt. Im einfachsten Fall ist der Nenner gleich. In diesem Fall werden die Zähler addiert und der Nenner wird übernommen.
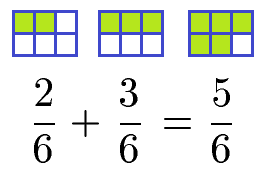
Weitere Beispiele auch zu Brüchen mit verschiedenen Nennern (= ungleichnamige Brüche) findest du unter Brüche addieren.
Rationale Zahlen subtrahieren:
Rationale Zahlen in Form von Kommazahlen bzw. Dezimalzahlen werden mit der schriftlichen Subtraktion berechnet. Dazu werden die Zahlen untereinander geschrieben, Komma unter Komma. Wie von der schriftlichen Subtraktion gewöhnt wird von hinten nach vorne Schritt für Schritt subtrahiert.
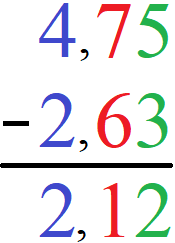
Weitere Beispiele und Erklärungen bekommst du unter unter Rechnen mit Dezimalzahlen. Liegen die rationalen Zahlen als Brüche vor gelten die Regeln der Bruchrechnung. Im einfachsten Fall sind die Nenner gleich. In diesem Fall werden die Zähler subtrahiert und der Nenner wird beibehalten.
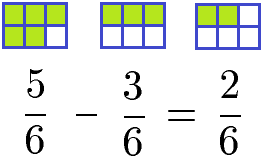
Weitere Erklärungen und Beispiele - auch zu unterschiedlichen Nennern - findest du unter Brüche subtrahieren.
Rationale Zahlen multiplizieren:
Die Multiplikation rationaler Zahlen in Form von Dezimalzahlen erfolgt mit der schriftlichen Multiplikation. Dazu wird zunächst schriftlich multipliziert als gäbe es kein Komma. Danach werden die Anzahl der Stellen nach dem Komma gezählt und das Komma entsprechend auch im Ergebnis gesetzt.
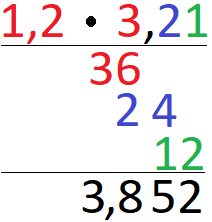
Weitere Erklärungen und Beispiele zur Multiplikation mit rationalen Zahlen findest du unter unter Rechnen mit Dezimalzahlen. Beim Rechnen mit rationalen Zahlen in Form von Brüchen wird einfach Zähler mal Zähler und Nenner mal Nenner gerechnet.
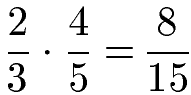
Weitere Erklärungen und Beispiele findest du unter Brüche multiplizieren.
Rationale Zahlen dividieren:
Die Division von rationalen Zahlen in Form von Dezimalzahlen wird mit der schriftlichen Division durchgeführt. Zunächst ein vorgerechnetes Beispiel:
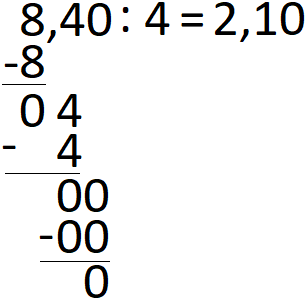
Ausführliche Beschreibungen zur Division von rationalen Zahlen in Dezimalform bekommst du unter unter Rechnen mit Dezimalzahlen.
Die Division von rationalen Zahlen in Form von Brüchen ist hingegen sehr einfach. Das Geteiltzeichen wird durch ein Malzeichen ersetzt. Dafür wird beim zweiten Bruch Zähler und Nenner vertauscht. Aus der Division wird eine Multiplikation die mit Zähler mal Zähler und Nenner mal Nenner gelöst wird.
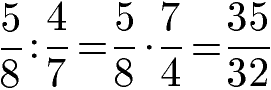
Weitere Erklärungen und Beispiele findest du unter Brüche dividieren. Werfen wir nun einen Blick auf die Rechengesetze zu rationalen Zahlen.
Rechengesetze bei rationalen Zahlen
Drei Rechengesetze sind ganz wichtig für den Mathematik-Unterricht: Kommutativgesetz, Assoziativgesetz und Distributivgesetz. Diese drei Rechengesetze können auf rationale Zahlen angewendet werden. Es spielt dabei keine Rolle, ob es sich um Brüche oder um Dezimalzahlen handelt.
Kommutativgesetz für rationale Zahlen:
Bei der Addition von Brüchen spielt die Reihenfolge der Summanden nach dem Kommutativgesetz keine Rolle für das Ergebnis.
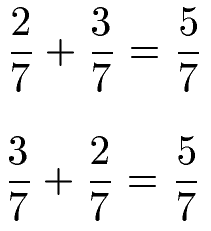
Das Kommutativgesetz besagt auch, dass die Reihenfolge der Zahlen bei der Addition von Dezimalzahlen keine Rolle für die Summe spielt.
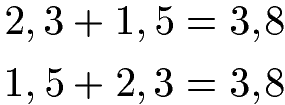
Bei der Multiplikation von Brüchen spielt die Reihenfolge der Faktoren nach dem Kommutativgesetz keine Rolle für das Ergebnis.
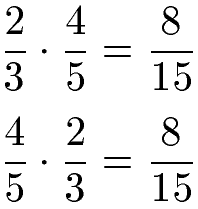
Das Kommutativgesetz besagt auch, dass die Reihenfolge der Zahlen bei der Multiplikation von Dezimalzahlen keine Rolle für das Produkt spielt.
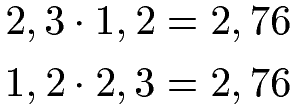
Assoziativgesetz für rationale Zahlen:
Nach dem Assoziativgesetz spielt die Reihenfolge der Addition von Dezimalzahlen keine Rolle für das Ergebnis.
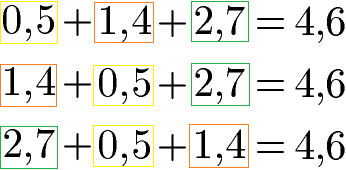
Das Assoziativgesetz gilt auch für Brüche: Die Reihenfolge der Brüche spielt für die Summe keine Rolle.
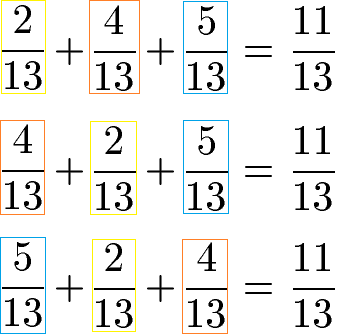
Das Assoziativgesetz für Dezimalzahlen besagt, dass die Reihenfolge für die Multiplikation von Dezimalzahlen keinen Einfluss auf das Ergebnis hat.
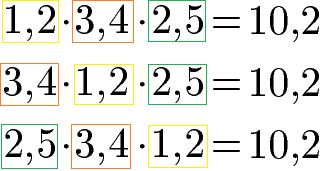
Nach dem Assoziativgesetz kann die Reihenfolge der Brüche bei einer Multiplikation beliebig vertauscht werden ohne das Produkt zu verändern.
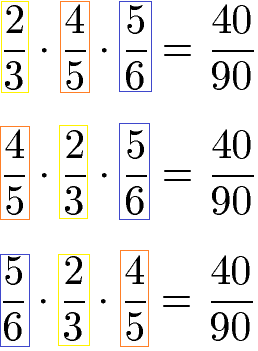
Distributivgesetz für rationale Zahlen:
Das Distributivgesetz kann dazu verwendet werden Klammern aufzulösen oder Klammern zu erzeugen. Dieses Rechengesetz kann auch für rationale Zahlen in Form von Dezimalzahlen bzw. Kommazahlen eingesetzt werden. Ein Beispiel zum Auflösen einer Klammer mit Dezimalzahlen.
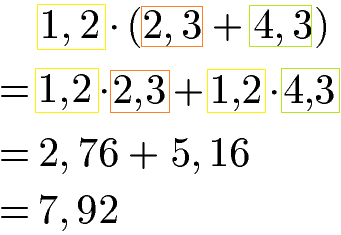
Das Distributivgesetz kann verwendet werden um Klammern mit Brüchen aufzulösen. Dazu wird der Bruch vor oder nach der Klammer mit allen Brüchen innerhalb der Klammer multipliziert.
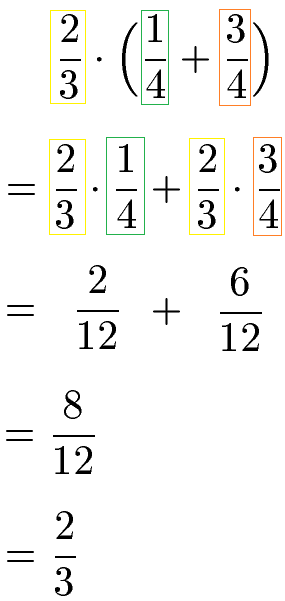
1846 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige: