Wie man den Umfang von einem Rechteck berechnet, lernst du in diesem Artikel mit Text und Video. Du erfährst mit welchen Formeln der Rechteck Umfang zu berechnen ist und bekommst Beispiele zum besseren Verständnis. Für Fortgeschrittene wird der Umfang des Rechtecks auch über die Fläche oder die Diagonale mit Formeln berechnet. Auf die Einheiten (Längeneinheiten) für die Berechnung wird ebenfalls eingegangen.
Ein Rechteck ist ein Viereck mit 4 Seiten. Die gegenüberliegenden Seiten sind dabei jeweils gleich lang und werden meistens mit a (hier rot) und b (hier blau) bezeichnet.
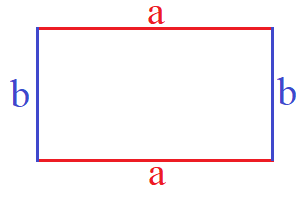
Der Umfang des Rechtecks gibt an, wie lange der Rand des Rechtecks ist. Stelle dir folgendes vor: Das Rechteck sei eine Matte auf dem Fußboden. Eine Ameise läuft nun den Rand der Matte von einer Ecke aus ab bis sie wieder die Startecke erreicht.

Der Umfang des Rechtecks ist damit a + b + a + b. Solche Zusammenhänge werden in der Mathematik mit Formeln angegeben. Die Formeln um den Umfang des Rechtecks zu berechnen und Beispiele sehen wir uns jetzt näher an.
Umfang Rechteck Formel mit Seitenlänge
Der Umfang des Rechtecks lässt sich im einfachsten Fall aus den Seitenlängen bestimmen. Dazu wird die Länge der Seite a verdoppelt und die Länge der Seite b wird verdoppelt. Beides wird addiert. Zwei Schreibweisen sind für diesen Zusammenhang möglich, Beispiele folgen weiter unten.
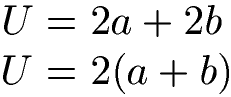
Der Umfang des Rechtecks wird in der Formel mit "U" abgekürzt. Die Variablen "a" und "b" stehen für die Längen der Seiten des Rechtecks. Alle Angaben sind Längenangaben. Bei den Einheiten werden meistens Zentimeter oder Meter verwendet. Weitere Einheiten und deren Umrechnung sehen wir uns am Ende des Artikels noch einmal an.
Umfang Rechteck Beispiel:
Der Umfang eines Rechtecks soll berechnet werden. Die Seitenlängen sind 20 cm und 30 cm. Wie lange ist der Umfang?

Wir setzen in die Formel für den Umfang a = 30 cm und b = 20 cm ein. Beachte bei der Berechnung die Regel Punkt vor Strich. Daher berechnen wir zuerst die Multiplikationen und im Anschluss die Addition. Da die Angaben in Zentimeter (cm) sind werden diese Einheiten ebenfalls bei der Berechnung verwendet.
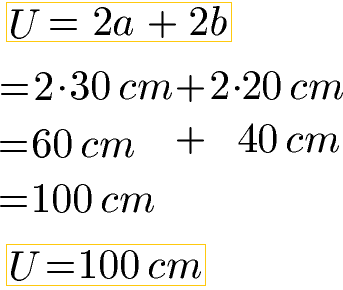
Ein Rechteck mit den Seitenlängen 60 Zentimeter und 40 Zentimeter hat einen Umfang von 100 Zentimeter, kurz 100 cm.
Umfang Rechteck Formel mit Fläche
Eine weitere Möglichkeit den Umfang des Rechtecks zu berechnen funktioniert mit der Fläche. Die Fläche - manchmal auch als Flächeninhalt bezeichnet - gibt an, wie groß der Inhalt des Rechtecks ist. In der nächsten Grafik ist dies Fläche grün eingezeichnet.
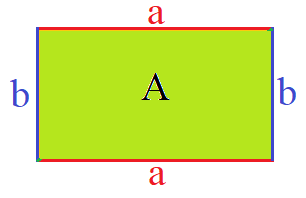
Der Umfang des Rechtecks lässt sich mit der Fläche und einer der beiden Seitenlängen berechnen. Kennst du die Fläche und die Länge der Seite b kannst du die obere Formel verwenden, um den Umfang zu berechnen. Kennst du die Fläche und die Seitenlänge a solltest du die untere Formel nehmen.
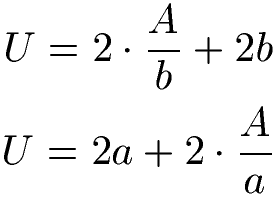
In den Formeln steht "U" für den Umfang des Rechtecks, "A" ist die Fläche des Rechtecks und "a" und "b" beschreibt die Länge der Seiten.
Umfang Rechteck Beispiel mit Fläche:
Ein Rechteck hat eine Fläche von 15 Quadratmeter (15 m2)und eine Seitenlänge von a = 3 m. Wie groß ist der Umfang des Rechtecks? Zur Berechnung verwenden wir die Formel mit der Fläche "A" und der Seitenlänge "a" und setzen alle Zahlen und Einheiten ein.
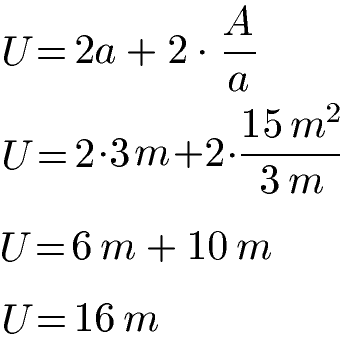
Achte bei der Berechnung darauf zuerst die Multiplikationen und den Bruch zu berechnen und erst danach die Addition.
Ein wichtiger Punkt sollte ebenfalls beachtet werden: Kommt bei der Fläche Quadratmeter (m2) sollten es Meter (m) bei den Seitenlängen sein. Sind es Quadratzentimeter (cm2) bei der Fläche sollten es Zentimeter (cm) bei den Seitenlängen sein. Falls nicht bitte erst die Einheiten umrechnen.
Umfang Rechteck Formel mit Diagonale
Der Umfang eines Rechtecks kann auch mit der Diagonalen berechnen werden. Die Diagonale ist die Strecke zwischen einer Ecke des Rechtecks und der gegenüberliegenden Ecke. Die Diagonale wird oft mit "d" bezeichnet. Da wir jedoch gleich mit dem Satz des Pythagoras rechnen werden wird hier "c" verwenden, wie man dies von der Hypotenuse her kennt.
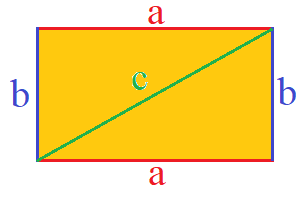
Um den Umfang des Rechtecks mit Hilfe der Diagonalen zu berechnen, brauchst du die Länge der Diagonalen und zusätzlich die Länge der Seite "a" oder "b". Die Formeln lauten:
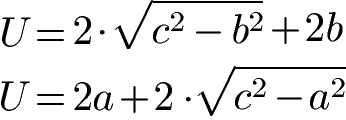
Umfang Rechteck Beispiel mit Diagonale:
Bei einem Rechteck ist die Diagonale 5 Zentimeter lang (c = 5 cm). Die Seitenlänge b sei 3 Zentimeter (b = 3cm). Wie lange ist der Umfang? Zur Lösung verwenden wir die Formel mit "c" und "b" um den Umfang zu berechnen. Wirf erst einmal einen Blick auf die Rechnung, unterhalb gibt es einige Erklärungen.
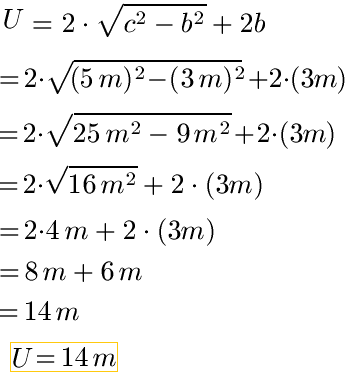
Hinweise zur Berechnung:
- Beim Quadrieren (c2 und b2) muss nicht nur die Zahl, sondern auch die Einheit quadriert werden.
- Beim Ziehen der Wurzel wird aus den Quadratmetern (m2) wieder Meter (m).
- Achte auf die Punktrechnung vor Strichrechnung.
Einheiten beim Umfang des Rechtecks und Volumen
Bei der Berechnung des Umfangs eines Rechtecks werden Längeneinheiten verwendet. Oft verwendete Längeneinheiten sind Kilometer, Meter, Dezimeter, Zentimeter und Millimeter. Zunächst solltest du zu jeder Einheit die Abkürzung kennen.
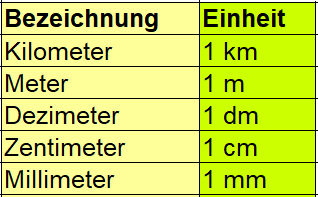
Bei der Berechnung müssen gleiche Einheiten verwendet werden. Liegt zum Beispiel die Seitenlänge "a" in Zentimeter vor und die Seitenlänge "b" in Meter, sollten zunächst beide Angaben in Zentimeter oder beide Angaben in Meter umgerechnet werden. Die nächste Grafik zeigt die Umrechnung der Einheiten untereinander.
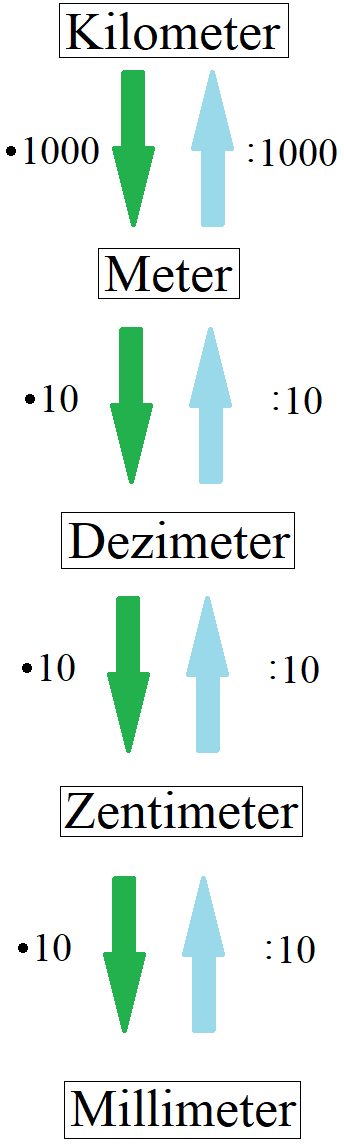
Solltest du weitere Erklärungen und Beispiele benötigen findest du diese unter Einheiten umrechnen.
Volumen Rechteck:
Im Zusammenhang mit Fläche und Umfang von einem Dreieck taucht oft auch die Frage nach dem Volumen eines Rechtecks auf. Da ein Rechteck ein ebenes Viereck ist, sprich keine Höhe (h = 0) hat, gibt es auch kein Volumen. Das Volumen eines Rechtecks ist 0.
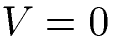
1840 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige: