Teilerfremd berechnen ▷ Beispiele

Teilerfremde Zahlen werden ab der 5. Klasse im Mathematik-Unterricht behandelt. Was teilerfremd bedeutet und wie man dies berechnen kann, bekommst du hier sehr einfach erklärt. Du lernst dabei wie du dies mit einer Teilermenge oder der Primfaktorzerlegung für den größten gemeinsamen Teiler prüfen kannst.

Zwei verschiedene Zahlen sind teilerfremd, wenn sie keine gemeinsamen Teiler außer der Zahl 1 haben. Als Beispiel nehmen wir einmal die Teiler der Zahlen 15 und 18. Für beide Zahlen wurden die Teiler in eine Teilermenge geschrieben.

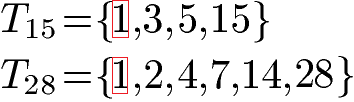
Wie du sehen kannst, taucht nur die Zahl 1 in beiden Mengen auf. Es gibt keinen weiteren Teiler in beiden Teilermengen. Daher sind die Zahlen 15 und 28 teilerfremd.

Teilerfremd prüfen mit Teilermenge

Es gibt grundsätzlich zwei Möglichkeiten Zahlen auf Teilerfremdheit zu überprüfen:

• Für kleine Zahlen setzen wir die Teilermenge ein.
• Für größere Zahlen setzen wir die Primfaktorzerlegung für den größten gemeinsamen Teiler (ggT) ein.

In diesem Abschnitt starten wir mit kleinen Zahlen und verwenden dazu die Teilermenge. Wir sehen uns dazu gleich noch ein einfaches Beispiel an. Falls du dieses Beispiel nicht verstehst, solltest du im Anschluss erst einmal einen Blick auf die Inhalte unter Teiler und Vielfache werfen.

Beispiel Teiler von 25 und 30:

Sind die Zahlen 25 und 30 teilerfremd? Dies kann man auch ohne Berechnung ganz schnell beantworten. Denn die 25 endet auf 5 und die 30 auf 0. Endet eine Zahl auf 5 oder 0 ist diese durch 5 ohne Rest teilbar. Daher wissen wir sofort das diese nicht teilerfremd sind. Die andere Möglichkeit besteht darin die Teiler der Zahlen in eine Teilermenge zu schreiben.

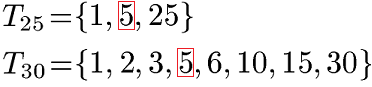
Sowohl die Teilermenge von 25 als auch von 30 beinhalten die Zahl 5. Die 5 ist daher ein Teiler von 25 und von 30, daher sind diese Zahlen nicht teilerfremd.

Die Berechnung der Teilermenge ist für sehr kleine Zahlen noch recht einfach. Für größere Zahlen wird dies jedoch sehr viel aufwendiger. Daher erfolgt die Prüfung auf Teilerfremdheit für große Zahlen mit einem anderen Verfahren. Wir zerlegen dazu die Zahlen in Primfaktoren und ermitteln den größten gemeinsamen Teiler (ggT).

Teilerfremd mit ggT

Ob zwei größere Zahlen teilerfremd sind lässt sich mit der Primfaktorzerlegung prüfen. Dazu zerlegen wir die zu untersuchenden Zahlen in eine Multiplikation möglichst kleiner Zahlen (Primzahlen), schreiben diese als Potenz und bilden den größten gemeinsamen Teiler (ggT). Dies klingt kompliziert, ist jedoch meistens gar nicht so schwer umzusetzen.

Als Beispiel soll geprüft werden, ob die Zahlen 32 und 42 teilerfremd sind oder nicht. Dazu zerlegen wir zunächst die Zahl 32 in Primfaktoren. Die 32 lässt sich zerlegen in 2 · 16. Die 16 zerlegen wir in 2 · 8 und die 8 in 4 · 2 und die 4 in 2 · 2. Wir erhalten die Zahl 2 insgesamt 5 Mal. Daher schreiben wir dies als Potenz mit 2⁵.

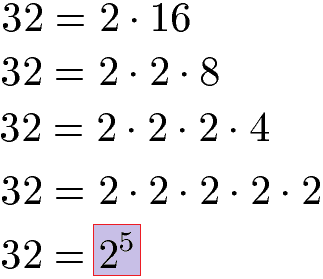
Die Primfaktorzerlegung führen wir auch für die Zahl 42 durch. Die 42 lässt sich zerlegen in 2 · 21 und die 21 zerlegen wir in 3 · 7. Das Ergebnis schreiben wir ebenfalls als Potenz.

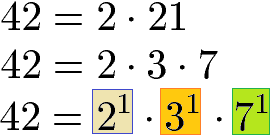
Um den größten gemeinsamen Teiler (ggT) zu finden sehen wir uns die Potenzschreibweise von 32 und 42 an. Die Potenzen mit 3 und 7 als Basis kommen nur in einer der beiden Zerlegungen vor. Diese sind daher für uns nicht wichtig. Die Potenz mit der Basis 2 kommt in beiden Zerlegungen vor mit 2⁵ und 2¹. Für den größten gemeinsamen Teiler (ggT) benötigen wir die kleinere Potenz, sprich 2¹.

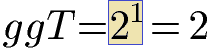
Der größte gemeinsame Teiler ist 2. Beide Zahlen lassen sich durch 2 teilen. Es existiert ein gemeinsamer Teiler neben der 1 und daher sind die Zahlen nicht teilerfremd.