Das Rechnen mit negativen Zahlen lernst du hier. Der Umgang mit Vorzeichen und Rechenzeichen (++, +-, -+, --) wird gezeigt und es werden Rechenregeln wie Punkt vor Strich und die Klammerrechnung mit negativen Zahlen durch Beispiele erklärt. Die Inhalte liegen als Text und als Video vor.
Um mit negativen Zahlen rechnen zu können, solltest du erst einmal Wissen, was negative Zahlen überhaupt sind und wie man diese am Zahlenstrahl bzw. der Zahlengerade darstellt. Falls du davon noch nie etwas gehört hast wirft bitte erst einen Blick in negative Zahlen im Alltag und Zahlengerade.
Für das Rechnen mit negativen Zahlen müssen bestimmte Rechenregeln beachtet werden. Zunächst wäre dabei der Umgang mit Rechenzeichen und Vorzeichen zu nennen.
Das Rechenzeichen gibt an, was gemacht werden soll: Addition (+), Subtraktion (-), Multiplikation (·) und Division (:). Das Vorzeichen gibt an, ob die Zahl positiv oder negativ ist (zum Beispiel +5 oder -5).
Treffen zwei Zeichen aufeinander werden diese zusammengefasst: Zwei gleiche Zeichen werden zu einem plus, verschiedene Zeichen zu einem minus.

In den nächsten Abschnitten sehen wir Beispiele zu Rechenzeichen und Vorzeichen an sowie allgemein das Rechnen mit negativen Zahlen. Dazu zählen auch die Regeln Punkt vor Strich und Klammerrechnung.
Addition negativer Zahlen
Beim Rechnen mit negativen Zahlen sind zunächst die 4 Grundrechenarten interessant. Starten wir mit der Addition negativer Zahlen. Im ersten Beispiel haben wir die positive Zahl 18. Danach findet sich das Zeichen für die Addition und dahinter die Zahl -20.
Mit anderen Worten: Auf die Zahl 18 wird die Zahl -20 addiert. Es treffen dabei Rechenzeichen (+) und Vorzeichen (-) aufeinander. Zwei verschiedene Zeichen werden zu einem Minuszeichen (-). Daher erhalten wir 18 - 20 = -2.
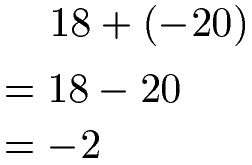
Im zweiten Beispiel haben wir erneut eine Addition (+) mit negativen Zahlen. In diesem Fall sind beide Zahlen (-10 und -20) negativ. Da mit + - zwei verschiedene Zeichen aufeinander treffen, wird daraus ein Minuszeichen. Von den -10 wird daher 20 abgezogen, ergibt -30.
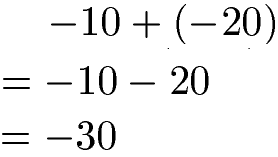
Im nächsten Abschnitt sehen wir uns die Subtraktion negativer Zahlen an.
Negative Zahlen subtrahieren
Das Subtrahieren negativer Zahlen funktioniert ähnlich wie die Addition negativer Zahlen. Zunächst fassen wir wieder Rechenzeichen und Vorzeichen zusammen. Aus minus und plus wird minus. Wir subtrahieren von der -15 daher die 5 und erhalten -20.
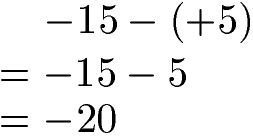
Im zweiten Beispiel treffen zwei Minuszeichen aufeinander: Von der negativen Zahl -15 subtrahieren wir die negative Zahl 5. Zwei Minuszeichen folgen aufeinander, daher werden diese zu einem Pluszeichen. Auf die -15 addieren wir aus diesem Grund 5 drauf und erhalten -10.
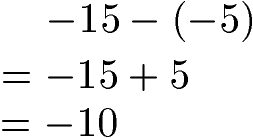
Dies waren die Grundrechenarten Addition und Subtraktion. In den nächsten Abschnitten geht es um die Multiplikation negativer Zahlen und die Division negativer Zahlen.
Multiplikation und Division negativer Zahlen
Bei der Multiplikation negativer Zahlen muss eine wichtige Regel der Mathematik beachtet werden: Zwei gleiche Vorzeichen ergeben ein positives Ergebnis, ansonsten ist das Produkt negativ.
Die nächsten vier Beispiele zeigen wie sich die Vorzeichen bei den Faktoren verändern und welchen Einfluss dies auf das Vorzeichen im Ergebnis (Produkt) hat.
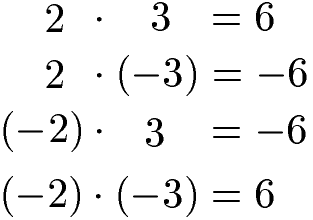
Bei der Division gilt diese Rechenregel ebenfalls: Zwei gleiche Vorzeichen ergeben ein positives Ergebnis, ansonsten ist das Ergebnis negativ. Die nächsten vier Aufgaben zeigen wie sich das Vorzeichen bei Dividend und Divisor verändert und welchen Einfluss dies auf das Vorzeichen im Ergebnis (Quotient) hat.
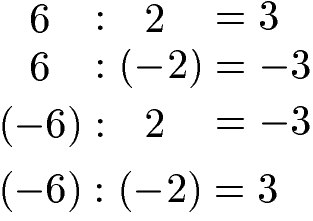
1754 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige: