Die Zinsrechnung lernst du in diesem Video. Du lernst wichtige Begriffe wie Kapital, Zinssatz und Dauer kennen und wie diese mit Formeln berechnet werden können. Einfache Beispiele mit Zahlen werden vorgerechnet und erklärt. Außerdem bekommst du eine Übersicht zu den Formeln der Zinsrechnung und wie diese umgestellt werden.
Die Zinsrechnung beschäftigt sich mit dem Anlegen von Geld. Es geht dabei darum wie viel Zinsen (= zusätzliches Geld) du von einer Bank oder einem anderen Kreditnehmer für das Leihen von Geld bekommst. Zunächst solltest du diese Begriffe zur Zinsrechnung kennen:
- Anfangskapital KA: Das Anfangskapital gibt an, wie viel Geld angelegt wird. Es ist die Menge an Geld vor der Verzinsung.
- Endkapital KE: Das Endkapital gibt an, wie viel Geld nach der Verzinsung vorhanden ist.
- Zinsen Z: Die Zinsen sagen aus, wie viel Geld hinzukommt für einen bestimmten Zeitraum.
- Zinssatz p%: Der Zinszahl gibt an, um wie viel Prozent sich das Geld vermehrt (mit Prozentzeichen).
- Zinszahl p: Die Zinszahl ist die Angabe vom Zinssatz ohne Prozentzeichen.
Sehen wir uns Formeln und Beispiele zur Zinsrechnung an.
Zinsrechnung für 1 Jahr
In den Grundlagen der Zinsrechnung geht es zunächst darum Geld für 1 Jahr anzulegen. Das Geld wird für 1 Jahr (= 12 Monate) einer Bank, einer anderen Person, einem Staat oder einem Unternehmen geliehen. Derjenige, der sich das Geld leiht, muss dafür Zinsen bezahlen. Wie hoch diese Zinsen sind hängt von der geliehenen Menge an Geld und dem Zinssatz ab.
Formel Zinsen und Kapital für 1 Jahr:
Um die Zinsen (Z) für ein Jahr zu berechnen, wird das Anfangskapital (KA) mit der Zinszahl (p) multipliziert und durch 100 geteilt. Rechnet man das Anfangskapital (KA) und die Zinsen (Z) zusammen, erhält man das Endkapital (KE).
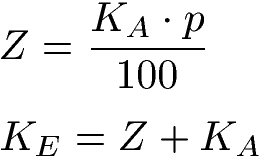
Beispiel: Zinsen für 1 Jahr
Ein Betrag von 2150 Euro wird für ein Jahr zu einem Zinssatz von 3 Prozent angelegt. Wie viele Zinsen fallen an? Wie viel Geld ist am Ende vorhanden?
Lösung: Wir setzen ein Anfangskapital von 2150 Euro in die Gleichung ein. Der Zinssatz ist p % = 3 %, daher ist die Zinszahl p = 3. Die Zinsen für 1 Jahr betragen 64,50 Euro. Diese Zinsen kommen auf das Anfangskapital drauf, die Endsumme beträgt damit 2214,50 Euro.
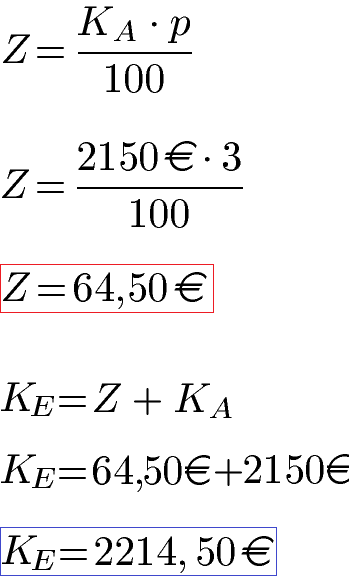
Formeln Zinszahl, Zinssatz und Anfangskapital
Die Formel zu den Jahreszinsen lässt sich nach der Zinszahl (p) und dem Anfangskapital (KA) umstellen.
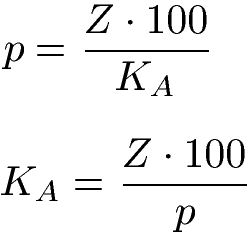
Der Zinssatz lässt sich sehr einfach in die Zinszahl umrechnen und umgekehrt. So entspricht der Zinssatz p % = 5 % der Zinszahl p = 5.
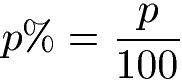
Beispiel: Zinssatz und Zinszahl berechnen
Ein Kapital von 2150 Euro wird für 1 Jahr angelegt. Dafür fallen 64,50 Euro an Zinsen an. Wie groß war der Zinssatz zu dem das Geld angelegt war?
Lösung: Das Startkapital beträgt KA = 2150 Euro. Die Zinsen werden mit Z = 64,50 Euro in die Formel eingesetzt. Mit der Formel lässt sich die Zinszahl zu p = 3 berechnen. Dies entspricht einem Zinssatz von 3 Prozent (p % = 3 %).
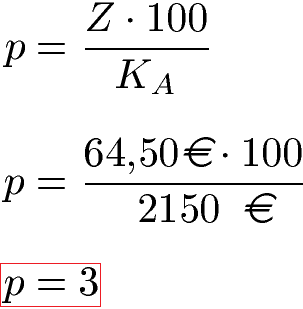
Weitere Beispiele findest du unter Jahreszinsen. Zinsen werden jedoch nicht nur für 1 Jahr berechnet, sondern auch für andere Zeiträume. Dies sehen wir uns in den nächsten Abschnitten an.
Monatszinsen: Zinsrechnung für Monate
Unter Monatszinsen versteht man die Zinsen, die für einige Monate bei der Anlage von Geld anfallen. Um die Zinsen für einige Monate zu berechnen, benötigst du das Geld zu Beginn der Geldanlage, das Anfangskapital (KA). Außerdem benötigst du den Zinssatz (p %) und die Anzahl der Monate (m). Die Formel für die Monatszinsen lautet:
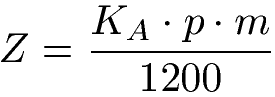
Beispiel Monatszinsen berechnen:
Ein Anfangskapital von 320 Euro wird für 7 Monate zu einem Zinssatz von 2 Prozent angelegt. Wie viele Zinsen fallen an? Lösung: Wir setzen KA = 320 Euro, p = 2 und m = 7 in die Gleichung ein. Damit ergeben sich Zinsen von 3,73 Euro.
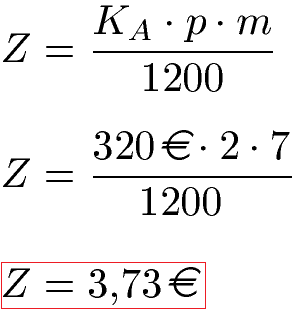
Monatszinsen: Formeln umstellen
Die Formel für die Monatszinsen lässt sich nach anderen Größen umstellen. Mit den nächsten Gleichungen kannst du direkt den Zinssatz, das Anfangskapital und die Monate berechnen.
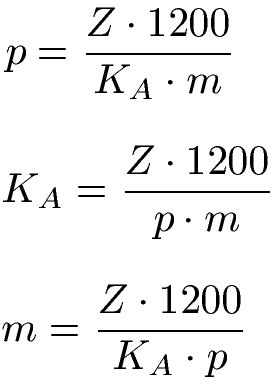
Beispiel: Monatsanzahl berechnen
Ein Geldbetrag von 320 Euro wird zu 2 Prozent angelegt und ergibt Zinsen von 3,73 Euro. Wie lange wurde das Geld angelegt? Lösung: Wir setzen die Angaben in die Formel ein und berechnen einen Zeitraum von 7 Monaten.
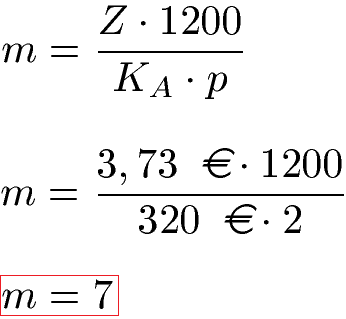
Weitere Erklärungen und Beispiele findest du unter Monatszinsen.
Tageszinsen: Zinsrechnung für Tage
Wird Geld für einige Tage angelegt fallen dabei Tageszinsen an. Um die Zinsen für einige Tage zu berechnen, benötigst du das Anfangskapital (KA), den Zinssatz (p %) und die Anzahl der Tage (t). Die Formel für die Zinsen von Tagen lautet:
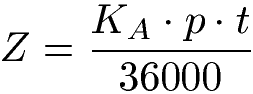
Beispiel: Formel Tageszinsen
Ein kleiner Geldbetrag von 210 Euro wird zu 2 Prozent für einen Zeitraum von 16 Tagen angelegt. Wie viele Zinsen fallen an? Lösung: Wir setzen die Angaben mit KA = 210 Euro, p = 2 und t = 16 ein und berechnen 19 Cent an Zinsen.
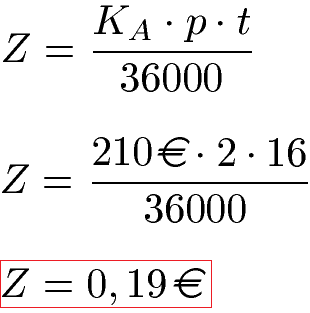
Formel: Zinssatz, Anfangskapital und Tage
Die Formel zu den Tageszinsen lässt sich nach der Zinszahl (Zinssatz), dem Anfangskapital und der Anzahl der Tage umstellen. Die Gleichungen bzw. Formeln sind diese.
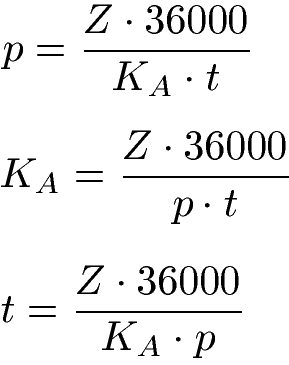
Beispiel: Anzahl Tage berechnen
Ein Anfangskapital von 300 Euro wird zu einem Zinssatz von 4 Prozent angelegt und bringt 0,40 Euro an Zinsen. Wie viele Tage wurde das Geld angelegt? Lösung: Wir setzen die Zahlen in die Formel ein und berechnen 12 Tage Anlagezeit.
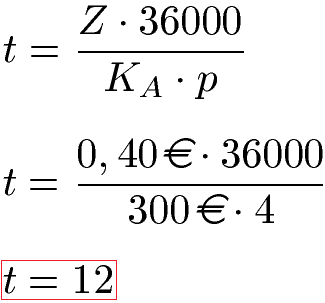
Weitere Erklärungen und Beispiele unter Tageszinsen.
Zinseszins: Zinsrechnung für Jahre
Der Zinseszins dient dazu die Zinsen für mehrere Jahre zu berechnen. Der Hintergrund: Wird Geld für 1 Jahr angelegt entfallen für diesen Zeitraum Zinsen. Aus 1000 Euro werden zum Beispiel 1020 Euro. Für das nächste Jahr werden nicht 1000 Euro, sondern 1020 Euro angelegt. Demnach verzinsen sich auch nicht 1000 Euro für das 2. Jahr, sondern 1020 Euro.
Die Formel zum Zinseszins sieht vor, dass das Endkapital (KE) berechnet wird. Für die Berechnung wird das Anfangskapital (KA), der Zinssatz (p %) und die Anzahl der Jahre (n) benötigt. Die Gleichung lautet:
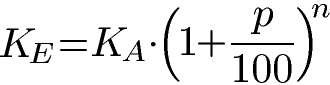
Beispiel: Zinseszins für 7 Jahre
Eine Summe von 50 Euro wird für 7 Jahre zu einem Zinssatz von 4 Prozent angelegt. Wie viel Geld liegt am Ende vor? Lösung: Wir setzen KA = 50 Euro, die Zinszahl p = 4 und die Anzahl der Jahre n = 7 in die Formel ein. Zuerst wird die Klammer berechnet, im Anschluss die Potenz. Das Ergebnis wird mit den 50 Euro multipliziert und ergibt ein Endkapital von 65,80 Euro.
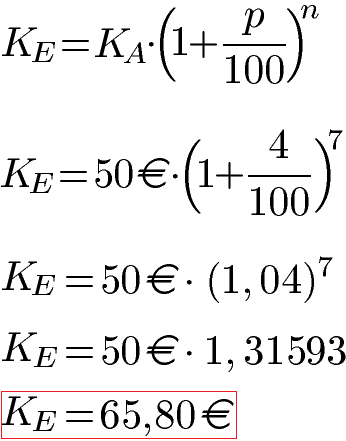
Formel Zinseszins umstellen:
Die Formel zum Zinseszins kann nach den anderen Größen umgestellt werden. Die Gleichung kann dabei nach dem Anfangskapital, der Zinszahl (Zinssatz) und der Anzahl der Jahre umgestellt werden. Die Gleichungen zum Zinseszins lauten damit wie folgt:
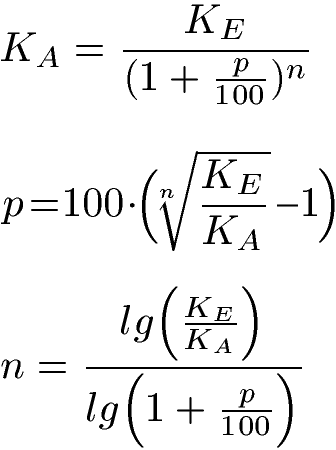
Weitere Erklärungen und Beispiele findest du unter Zinseszins.
Zinsrechnung Formeln Übersicht
Eine Übersicht zu den Formeln der Zinsrechnung bekommst du in diesem Abschnitt. Zunächst ein Überblick zu den Variablen, danach die Gleichungen.
Zinsen für 1 Jahr:
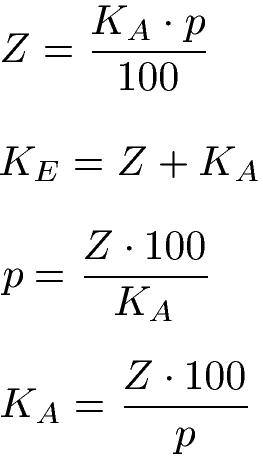
Zinsen für einige Monate:
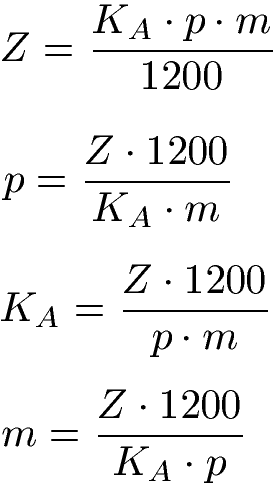
Zinsen für einige Tage:
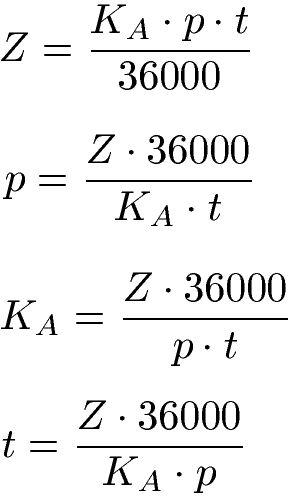
Zinsen für mehrere Jahre:
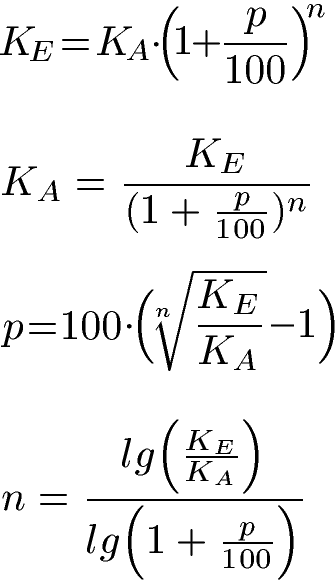
Zinssatz und Zinszahl umrechnen:
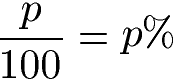
Mehr zur Zinsrechnung:
- Jahreszinsen
- Monatszinsen
- Tageszinsen
- Zinseszins
- Zinsrechnung Aufgaben / Übungen
- Zur Mathematik-Übersicht
1782 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige: