Integralrechnung

Die Integralrechnung ist die Umkehrung der Differentiation und dient zur Berechnung von Flächen. Mit der Integralrechnung und mit den entsprechenden Integrationsregeln befassen wir uns in diesem Artikel.

Hinweis: Die Inhalte dieses Artikels liegen auf Wunsch auch als Video vor: Grundlagen + Summenregel Video, Elementare Integrationsregeln Video, Partielle Integration Video und Flächenberechnung Video.

In diesem Artikel gehen wir auf die folgenden Themen der Integralrechnung näher ein:

1. Integralrechnung: Grundlagen und Summenregel
2. Elementare Integrationsregeln
3. Integralrechnung mit Integrationsgrenzen
4. Formelsammlung zur Integralrechnung
5. Fläche und Integralrechnung

1. Integralrechnung: Grundlagen und Summenregel

Im Folgenden zeigen wir euch, was es mit der Summenregel der Integralrechnung auf sich hat. Ziel ist es, die Fläche unter einer Funktion  zu berechnen. Wir beginnen dabei mit der Untersumme. Schaut euch einmal die folgende Grafik an:

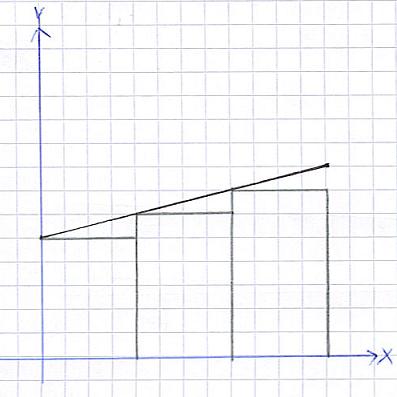
Obersumme und Untersumme:

In schwarz wird die Funktion dargestellt. Um die Fläche unter dieser zu berechnen, wurden Rechtecke eingezeichnet ( mit einer Breite von 2cm ). Wir ihr sicher wisst: Die Fläche eines Rechtecks berechnet sich aus Länge mal Breite. Man kann somit die Fläche aller Rechtecke ausrechnen und zusammen addieren. So erhält man die Fläche unter einer Funktion. Allerdings entsteht hier ein kleiner Fehler: Wie ihr sehen könnt, fehlt ein kleines Stück Fläche zwischen den Rechtecken und der Funktion. Es "fehlt" also Fläche. Dies war die Untersumme.

Als nächstes beschäftigen wir uns mit der Obersumme. Die Vorgehensweise ist sehr ähnlich zur Untersumme. Nur hier werden die Rechtecke etwas größer angesetzt. Werft aber erst einmal einen Blick auf die folgende Grafik:

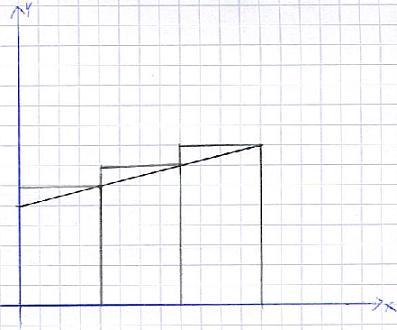
Es werden also erneut Rechtecke erzeugt. Deren Flächeninhalte ist ebenfalls Länge mal Breite. Und die einzelnen Rechtecke werden zu einer Gesamtsumme addiert. Nur hier ist die Summe größer als die eigentliche Fläche. Somit hat die Untersumme eine Fläche geliefert, die zu klein ist. Die Obersumme hingegen hat eine Fläche geliefert, die zu groß ist.

Exakte Fläche bestimmen

Sowohl die Obersumme, als auch die Untersumme haben ein "etwas" falsches Ergebnis geliefert. Das korrekte Ergebnis liegt irgendwo dazwischen. Aber wie bekommt man das richtige Ergebnis raus? Die Antwort ist eigentlich recht einfach: Es müssen mehr Rechtecke eingesetzt werden. Je mehr Rechtecke ihr habt, desto kleiner sind die fehlenden Flächen bzw. die Flächen, die zu groß sind. Ihr nähert euch damit dem "realen" Verlauf der Funktion viel besser an. Habt ihr praktisch unendlich viele Rechtecke, erhaltet ihr das Integral!

Allerdings ist es viel zu umständlich, eine große Anzahl an Rechtecken ein zu zeichnen, deren Fläche zu berechnen und das Ganze auf zu summieren. Aus diesem Grund, haben Mathematiker sich Gedanken gemacht, wie man dies einfacher lösen kann. Die Lösung lautet: Mittels einiger Regeln die Funktion integrieren und dadurch die Fläche zu erhalten. Wie diese Regeln funktionieren, lernt ihr ab dem nächsten Abschnitt der Integralrechnung.

2.Elementare Integrationsregeln

Stammfunktion:

Ihr kennt mit Sicherheit noch Funktionen. Da gab es zum Beispiel: f(x) = y = 2x oder f(x) = y = 2x³ + 3x. Und dann gab es die Ableitungen dazu, zum Beispiel f'(x) = y' = 2 oder f'(x) = y' = 6x² + 3. Beim Integrieren gehen wir in die umgekehrte Richtung. Wir haben eine Funktion und integrieren diese. Das Ergebnis ist eine Stammfunktion. Also nochmal zum mitschreiben: Wir haben eine Funktion y = f(x)= ____ und suchen die Stammfunktion Y = F(x) = ____.

Noch ein Hinweis: Wir beginnen hier nun mit den Integrationsregeln ohne dabei Integrationsgrenzen zu beachten! Es geht hier erst einmal darum, die Stammfunktion zu finden. Die Grenzen setzen wir anschließend im Bereich Flächenberechnung mit ein.

Integralrechnung: Konstante integrieren / Potenzregel

Beginnen wir bei der Integralrechnung mit der Potenzregel. Dabei wird hier zunächst eine Konstante integriert:

• f(x) = 2 und damit F(x) = 2x + C
• f(x) = 5 und damit F(x) = 5x + C
• f(x) = 8 und damit F(x) = 8x + C

Merke: Eine Konstante wird integriert, in dem man an die Konstante ein "x" angehängt und +C schreibt. Das C steht dabei für eine beliebige Zahl. Lasst dieses C erst einmal so stehen, wie es ist. Der Grund: Leitet ihr F(x) = 2x + 2 oder F(x) = 2x + 5 bzw. allgemein F(x) = 2x + C ab, erhaltet ihr wieder f(x) = 2.

Potenzregel:

Nun möchten wir Funktionen wie zum Beispiel f(x) = 2x  oder f(x) = 3x² integrieren. Dafür benutzen wir die Potenzregel, die wie folgt aussieht:

Die Anwendung der Potenzregel ist eigentlich recht simpel. Seht euch die Hochzahl der Funktion an, die ihr integrieren wollt. Addiert zu dieser die Zahl 1 und ihr habt den neuen Exponenten und die neue Zahl unterhalb des Bruches. Ein paar Beispiele:

Summenregel:

Wie auch bei der Summenregel der Differentation gibt es bei der Integralrechnung auch eine Summenregel, die sehr ähnlich aussieht. Diese besagt, dass ihr Gliedweise integrieren dürft. Wie immer sind einige Beispiele für das Verständnis vermutlich am besten:

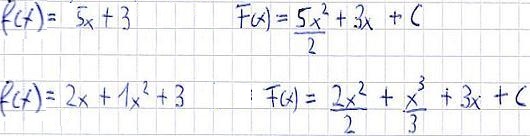
Partielle Integration ( Integralrechnung )

Soll ein Produkt integriert werden, wendet man die so genannte partielle Integration - oft auch Produktintegration - an. Wie dies funktioniert, lernt ihr in diesem Artikel aus dem Bereich Mathematik. Ich hoffe ihr erinnert euch an die Produktableitung ( Differentation ). So etwas ähnliches gibt es auch bei der Integration und wird als partielle Integration bezeichnet. Es folgt zunächst die allgemeine Formel, im Anschluss gibt es einige Beispiele.

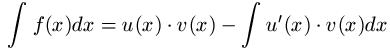
Partielle Integration Beispiel:

Zeit für ein paar Beispiele um die partielle Integration der Integralrechnung zu zeigen. Dazu gleich eine kleine Warnung:  Ihr müsst am Anfang u und v' festlegen. Wählt ihr diese falsch herum aus, könnt ihr die Aufgabe unter Umständen nicht mehr lösen. Tauscht in diesem Fall u und v' einmal gegeneinander aus und versucht es erneut. Es folgen nun zwei Beispiele und eine allgemeine Anleitung:

Beispiel 1:

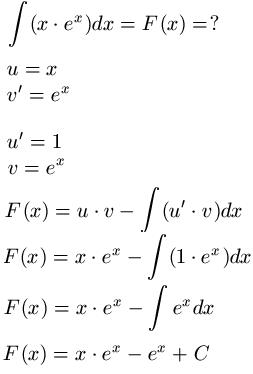
Anleitung partielle Integration:

• Wählt u und v'  für die Funktion eurer Aufgabe
• Bildet damit u' und v
• Setzt dies in die Formel der partiellen Integration ein
• Vereinfacht die Rechnung
• Löst das neu entstandene Integral
• Fasst die Lösung zusammen

3. Integralrechnung mit Integrationsgrenzen

Zeichnet man eine Funktion, so ergibt das oftmals einen sehr "langen" Verlauf. Jetzt will man natürlich nicht die komplette Fläche unter einer Funktion erhalten, die ist oftmals unendlich. Sondern nur die Fläche in einem gewissen Abschnitt. Deshalb setzt man so genannte Integrationsgrenzen. Schaut euch dazu erst einmal die folgende Grafik an:

Die Integrationsgrenzen werden meist mit a und b bezeichnet, wobei a die "untere" Integrationsgrenze und "b" die "obere" Integrationsgrenze bezeichnen. Heißt auf gut Deutsch: Die Fläche unter der Funktion von a bis b ist gesucht. Um diese zu bekommen müsst ihr wie folgt vorgehen:

• Integriert die Funktion mittels der Integrationsregeln
• Die Konstante "C" wird 0 gesetzt, sprich sie verschwindet
• Die Funktion mit oberer Grenze minus Funktion mit unterer Grenze berechnen

Beispiel:

Erklärungen: Die Funktion wird zunächst integriert. Die Stammfunktion wird in Klammern gesetzt und die Integrationsgrenzen werden an diese angetragen. Danach wird die Funktion ausgerechnet mit dem oberen Grenzwert: Setzt man die 1 in die Gleichung ein, erhält man ein Drittel. Danach wird ein minus "-" gesetzt". Hinter diesem wird der Funktionswert für die untere Grenze gebildet. Setzt man die 0 ein, ergibt sich eine Null. Dies ergibt ein Drittel als Gesamtergebnis.

4. Formelsammlung zur Integralrechnung

Hier findet ihr eine Tabelle / Formelsammlung um die Integralrechnung möglichst einfach durchzuführen. Druckt euch diese am Besten aus und seht beim Lösen von Aufgaben in die Tabelle.

5. Fläche und Integralrechnung

Zur Erinnerung: Mit der Integralrechnung lässt sich die Fläche unter einer Funktion bestimmen. Mit diesem Wissen versuchen wir im nun folgenden für ein einfaches Beispiel die Fläche zwischen den Graphen zweier Funktionen zu berechnen. Schaut euch dazu einmal die folgende Grafik an:

Folgendes gibt es bei dieser Grafik zu verstehen:

• Wir haben zwei Funktionen, die mit f(x) und g(x) bezeichnet werden
• Diese beiden Funktionsgraphen schneiden sich in den Punkten x₁ und x₂
• Die grüne Fläche ist die Fläche, welche die beiden Funktionsgraphen einschließen
• Die Funktion f(x) liegt zwischen den Schnittpunkten stets oberhalb von g(x)

Überlegung: Berechnen wir die Fläche unter g(x) und addieren die grüne Fläche drauf, erhalten wir die Fläche unter f(x). Oder anders ausgedrückt: Berechnen wir die Fläche unter f(x) und ziehen die Fläche unter g(x) ab, erhalten wir die grüne Fläche.

WICHTIG: Es bringt bei der Berechnung von Flächen zwischen Funktionsgraphen gar nichts, einfach irgendwelche Formeln stur auswendig zu lernen. Die Aufgaben können so verschieden gestellt werden, dass ihr mit bloßen Einsetzen in irgend eine Formel schnell zum falschen Ergebnis kommen würdet.

Beispiele: Flächen berechnen

Im nun Folgenden schauen wir uns verschiedene Beispiele zur Berechnung der Flächen an. Für das erste Beispiel geben wir dafür auch eine Beispielrechnung an. Für die anderen Beispiele beschränken wir uns vorerst auf die Idee zur Berechnung der Flächen.

Beispiel 1:

Die Fläche zwischen zwei Funktionsgraphen soll mit der Integralrechnung bestimmt werden. Deren Gleichungen lauten f(x) = x² - 8x + 17 und g(x) = -x + 7. Zur besseren Übersicht wurde eine Skizze angefertigt:

Um die Integrationsgrenzen zu erhalten, müssen wir die Schnittpunkte der beiden Funktionsgraphen finden.  Danach berechnen wir die Flächen unter den jeweiligen Funktionsgraphen. Deren Differenz ist die gesuchte Fläche. Das sieht dann so aus:

Nochmal zum mitdenken:

• Um die Integrationsgrenzen zu erhalten, haben wir die beiden Schnittpunkte der Funktionsgraphen berechnet
• Wir haben innerhalb dieser Grenze die Fläche unter g(x) berechnet
• Wir haben innerhalb dieser Grenze die Fläche unter h(x) berechnet
• Die Differenz ist die gesuchte, grün eingezeichnete Fläche

Es folgen einige weitere Beispiele, welche die Berechnung von Flächen zwischen Kurven zeigen. Um den Artikel nicht extrem in die Länge zu ziehen, wird bei diesen jedoch nur auf den allgemeinen Lösungsweg eingegangen.

Beispiel 2:

Kommen wir zu einem weiteren Beispiel, an dem die prinzipielle Denkweise verdeutlicht werden soll:

Zur Berechnung der Fläche müsste man wie folgt vorgehen:

• Die Funktionsgraphen haben keine Schnittpunkte, sondern werden in unserem Beispiel von x₁ und x₂ begrenzt.
• Die Fläche unter f(x) in den Grenzen wird berechnet. Dazu wird das Integral in den Grenzen x₁ und x₂ wie gewohnt für f(x) berechnet
• Die Fläche über g(x) wird berechnet. Dazu wird das Integral in den Grenzen x₁ und x₂ wie gewohnt für g(x) berechnet. Rechnerisch erhält man eine negative Fläche. Man nimmt von diesem Wert jedoch den Betrag.
• Die Fläche unter f(x) und der Betrag der Fläche unter g(x) in den Grenzen x₁ und x₂ werden addiert und bilden den gesamten Flächeninhalt.

Beispiel 3:

Unser nächstes Beispiel wird noch ein Stück komplizierter. Doch schaut euch zunächst einmal die folgende Grafik an:

Zur Berechnung der Fläche müsste man wie folgt vorgehen:

• Die Funktionen f(x) und g(x) schneiden sich in diesem Beispiel drei mal. Die Schnittpunkte müssen wie in Beispiel 1 berechnet werden
• Die linke grüne Fläche berechnet sich ähnlich wie in Beispiel 1: Die Flächen unter f(x) und g(x) werden in den Grenzen x₁ und x₂ jeweils berechnet. Die Differenz der Flächen ist die linke, grüne Fläche.
• Die rechte grüne Fläche berechnet sich ähnlich wie in Beispiel 1: Die Flächen unter f(x) und g(x) werden in den Grenzen x₂ und x₃ jeweils berechnet. Die Differenz der Fläche ist die rechte, grüne Fläche.

Links:

• Zur Mathematik-Übersicht