Integrieren: Stammfunktion, Potenzregel und Summenregel

In diesem Abschnitt beschäftigen wir uns mit dem Finden von Stammfunktionen und den grundlegenden Integrationsregeln. Dabei konzentrieren wir uns zunächst auf die Faktorregel und die Summenregel.

Zunächst eines vorweg: Wer noch nicht weiß, worum es bei der Integration überhaupt geht, der sollte erst einmal unseren Artikel Grundlagen der Integration durcharbeiten. Dieses Wissen wird benötigt, um zu verstehen worum es sich bei einer Stammfunktion überhaupt handelt und wie man diese findet.

Stammfunktion

Ihr kennt mit Sicherheit noch Funktionen. Da gab es zum Beispiel: f(x) = y = 2x oder f(x) = y = 2x³ + 3x. Und dann gab es die Ableitungen dazu, zum Beispiel f'(x) = y' = 2 oder f'(x) = y' = 6x² + 3. Beim Integrieren gehen wir in die umgekehrte Richtung. Wir haben eine Funktion und integrieren diese. Das Ergebnis ist eine Stammfunktion. Also nochmal zum mitschreiben: Wir haben eine Funktion y = f(x) und suchen die Stammfunktion Y = F(x).

Noch ein Hinweis: Wir beginnen hier nun mit den Integrationsregeln ohne dabei Integrationsgrenzen zu beachten! Es geht hier erst einmal darum, die Stammfunktion zu finden. Die Grenzen setzen wir anschließend ein. Wir wenden uns den Integrationsgrenzen im Kapitel Flächenberechnung zu.

Konstante integrieren / Potenzregel

Beginnen wir bei der Integration mit der Potenzregel. Dabei wird hier zunächst eine Konstante integriert:

• f(x) = 2 dx -> F(x) = 2x + C
• f(x) = 5 dx -> F(x) = 5x + C
• f(x) = 8 dx -> F(x) = 8x + C

Merke: Eine Konstante wird integriert, in dem man an die Konstante ein "x" angehängt und +C schreibt. Das C steht dabei für eine beliebige Zahl. Lasst dieses C erst einmal so stehen, wie es ist. Der Grund: Leitet Ihr 2x + 2 oder 2x + 5 bzw. allgemein 2x + C ab, erhaltet ihr wieder f(x) = 2.

Potenzregel:

Nun möchten wir Funktionen wie zum Beispiel f(x) = 2x  oder f(x) = 3x² integrieren. Dafür benutzen wir die Potenzregel, die wie folgt aussieht:

Die Anwendung der Potenzregel ist eigentlich recht simpel. Seht euch die Hochzahl der Funktion an, die ihr integrieren wollt. Addiert zu dieser die Zahl 1 und ihr habt den neuen Exponenten und die neue Zahl unterhalb des Bruches. Ein paar Beispiele:

Noch eine kleine Anmerkung: Im Allgemeinen schreibt man hinter die Funktion noch ein "dx", also zum Beispiel f(x) = ( 5x ) dx. Dies bedeutet, dass die Funktion nach x integriert wird. Um jetzt mathematisch korrekt zu arbeiten, werden wir diese Schreibweise in den folgenden Beispielen auch einsetzen.

Summenregel

Wie auch bei der Summenregel der Differentation gibt es bei der Integration auch eine Summenregel, die sehr ähnlich aussieht. Diese besagt, dass ihr Gliedweise integrieren dürft. Wie immer sind einige Beispiele für das Verständnis vermutlich am Besten:

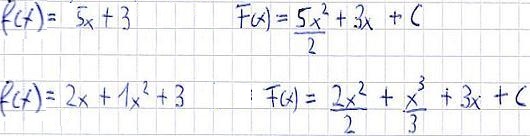
Links:

• Weiter zur partiellen Integration
• Zur Integration-Übersicht
• Zur Mathematik-Übersicht