Komplexe Zahlen Multiplikation / multiplizieren

Wie man komplexe Zahlen multiplizieren kann lernt ihr in diesem Artikel. Ich zeige dabei kurz den allgemeinen Zusammenhang für die Berechnung, dann einige Beispiele bzw. Aufgaben und gebe noch ein paar allgemeine Informationen. Dieser Artikel gehört zu unserem Bereich Mathematik.

In dem Artikel komplexe Zahlen Grundlagen haben wir uns bereits mit ein paar Grundlagen zu den komplexen Zahlen befasst. Nun gehen wir ans Rechnen mit komplexen Zahlen. Dabei sehen wir uns in diesem Artikel die Multiplikation von komplexen Zahlen an. Als Erstes in Kurzform der allgemeine Zusammenhang, dann geht es an Beispiele.

Allgemeiner Zusammenhang:

• Es sei: z₁ = x₁ + iy₁ und z₂ = x₂ + iy₂
• z₁ · z₂ = (x₁x₂ - y₁y₂) + i(x₁y₂ + x₂y₁)

Komplexe Zahlen Multiplikation

Sehen wir uns zum besseren Verständnis ein paar Beispiele an.

Beispiel 1:

Berechnet werden soll (5 - 2i) multipliziert mit (3 + 4i). Hier zunächst die Rechnung, die Erklärungen folgen unterhalb.

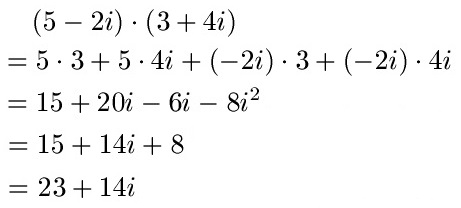
Wir multiplizieren zunächst die Klammern aus, so wie man das aus der Schule bereits kennt. Im Anschluss fassen wir zusammen. Wir erhalten bei diesen Maßnahmen ein -8i². In den Grundlagen haben wir gelernt, dass i² = -1 ist. Setzen wir für i² nun -1 ein wird aus -8i² eine +8. Wir können dann noch einmal vereinfachen und erhalten 23 + 14i als Ergebnis.

Beispiel 2:

Und noch ein Beispiel: 2 - 4i wird mit -3 + 5i multipliziert. Auch hier zunächst die Rechnung und im Anschluss die Erklärung.

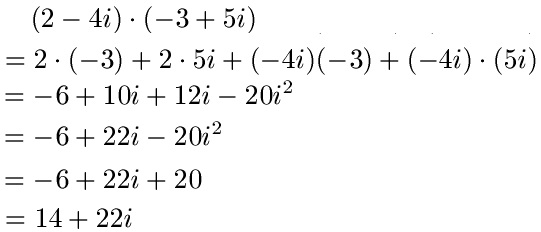
Die Vorgehensweise entspricht der aus dem 1. Beispiel. Auch hier multiplizieren wir zunächst aus und vereinfachen. Da auch hier i² = -1 gilt wird aus den -20i² wieder + 20. Im Anschluss wird dies wieder zusammengefasst zu 14 + 22i.

Komplexe Zahlen Multiplikation Hinweise:

• Multipliziert man zwei komplexe Zahlen so ist das Ergebnis ebenfalls eine komplexe Zahl.
• Für die Multiplikation gelten das Kommutativgesetz und das Assoziativgesetz.
• Auch gilt für komplexe Zahlen das Distributivgesetz.
• Wichtig ist den Zusammenhang i² = -1 stets im Kopf zu behalten.

Weitere Links:

• Komplexe Zahlen Übersicht
• Zur Mathematik-Übersicht