Kreisdiagramm

Mit dem Kreisdiagramm der Prozentrechnung befassen wir uns in diesem Artikel der Mathematik. Wir erklären euch dabei, was man unter einem Kreisdiagramm versteht und wie man dieses aufbaut. Für alle, die mit der Prozentrechnung noch zu kämpfen haben, finden sich weitere Informationen im Anschluss.

In den Medien sucht man oft nach übersichtlichen Methoden, Prozentangaben optisch gut darzustellen. Eine Möglichkeit dazu sind so genannte Kreisdiagramme. Dazu zeichnet man einen Kreis, in dem die Flächen entsprechend der Anteile an 100 Prozent dargestellt werden. Zum besseren Verständnis folgt dazu ein einfaches Beispiel.

Beispiel:

Ein Restaurant analysiert, welche Gerichte von den Kunden am meisten bestellt werden. Dabei wurden folgende Werte ermittelt:

• Schnitzel: 30 Prozent
• Pizza: 40 Prozent
• Salate: 10 Prozent
• Sonstiges: 20 Prozent

Diese Werte werden in ein Kreisdiagramm eingetragen:

Oftmals werden in den Medien die einzelnen Bereiche in verschiedenen Farben dargestellt. Für eine genaue Darstellung muss man die jeweilige Sektorgröße als Winkel folgendermaßen berechnen:

Prozentrechnung Grundlagen

Die Prozentrechnung dient dazu, einen Anteil an einem Ganzen darzustellen. So stellt 1% den hundertsten Anteil dar, 15% stellt 15 : 100 eines Ganzen da und 100% ist das Ganze, denn 100% : 100% = 1. Wie man sehen kann, ist die Prozentrechnung sehr nahe an die Bruchrechnung angelehnt. Dies wollen wir uns an dem folgenden Beispiel noch einmal kurz verdeutlichen.

Beispiel:

Herr A. möchte ein Grundstück für 120.000 Euro verkaufen. Ein Käufer verhandelt mit Herr A. und erhält einen Rabatt. Der Käufer muss nur noch 80% des angesetzten Wertes bezahlen. Wie viel muss der Kunde bezahlen?

Lösung: Der Preis des Grundstücks wird mit der Prozentangabe multipliziert, den der Kunde noch bezahlen muss. Das Ergebnis wird durch 100 Prozent dividiert. Dies sieht wie folgt aus:

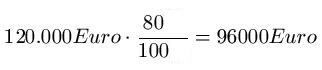
Prozentsatz Formel:

Die Einleitung dieses Artikels sollte euch hoffentlich einen kurzen Einblick in die Grundlagen der Prozentrechnung gegeben haben. Dieser Abschnitt soll nun wichtige Begriffe erklären. Diese lauten: Prozentwert, Grundwert und Prozentsatz. Der Zusammenhang zwischen dem Grundwert G, dem Prozentwert W und dem Prozentsatz p sieht dabei wie folgt aus.

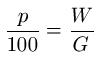
Links:

• Zur Mathematik-Übersicht