Linearfaktorzerlegung / Abspalten Linearfaktor

In diesem Artikel geht es um die Linearfaktorzerlegung bzw. das Abspalten eines Linearfaktors. Dies wird durch allgemeine Vorgehensweisen und Beispiele gezeigt. Dieser Artikel gehört zu unserem Bereich Mathematik.

Mit der Linearfaktorzerlegung bzw. dem Abspalten eines Linearfaktors befassen wir uns in diesem Artikel. Um die folgenden Inhalte verstehen zu können, müsst ihr jedoch wissen was eine Nullstelle ist und wie man diese findet. Dazu setzen wir PQ-Formel, Mitternachtsformel, Polynomdivision etc. ein. Wer damit noch Probleme hat, findet Hilfestellungen in den nun verlinkten Artikeln. Alle anderen können gleich mit der Linearfaktorzerlegung loslegen:

• PQ-Formel
• Mitternachtsformel
• Polynomdivision

Erklärung als Video:
Dieses Thema liegt auch als Video vor. In diesem werden typische Aufgabenstellungen, ein allgemeiner Lösungsweg, Beispiele und Tipps vorgestellt. Per Button kann auch in den Vollbildmodus gewechselt werden. Das Video ist auch direkt in der Sektion Linearfaktorzerlegung Video aufrufbar. Bei Abspielproblemen hilft der Artikel Video Probleme.

Polynom in Linearfaktoren zerlegen

Wie man ein Polynom in Linearfaktoren zerlegen kann sehen wir uns gleich an. Stellt sich noch die Frage, was die Linearfaktorzerlegung eigentlich bringt? Nun mit dem Ergebnis kann man oftmals leichter weiterrechnen und man sieht an diesem sofort wo die Nullstellen zu finden sind. Prinzipiell gilt: Besitzt eine Polynomfunktion an der Stelle x₁ eine Nullstelle, so kann man die Funktion auch in der Form f(x) = ( x - x₁ ) · f₁(x) darstellen. Man bezeichnet ( x - x₁ ) als Linearfaktor und f₁(x) als erstes reduziertes Polynom. Von dem reduzierten Polynom kann man unter Umständen wieder Linearfaktoren abspalten. Bevor wir uns Beispiele zum Abspalten eines Linearfaktors bzw. zur Linearfaktorzerlegung ansehen gibt es erst einmal eine allgemeine Liste um die Vorgehensweise zu beschreiben.

Vorgehensweise:

1. Nullstelle bzw. Nullstellen suchen
2. Linearfaktoren aufschreiben
3. In Produktdarstellung bringen
4. Eventuell Probe zur Kontrolle

Beispiel 1:

Gegeben sei f(x) = x² - 2x - 8. Es soll eine Zerlegung in Linearfaktoren durchgeführt werden. Lösung:

• Wir müssen die Gleichung x² - 2x - 8 = 0 lösen. Mit der PQ-Formel erhalten wir x₁= 4 und x₂ = -2.
• Die Linearfaktoren lauten damit ( x - 4 ) und ( x + 2 ).
• Wir erhalten damit f(x) = ( x - 4 ) ( x + 2 ) für die Produktdarstellung
• Probe: ( x - 4 ) ( x + 2 ) = x² - 2x - 8.

Beispiel 2:

Geben sei f(x) = x² + 2x + 1. Eine Zerlegung in Linearfaktoren soll durchgeführt werden. Lösung:

• Wir müssen x² + 2x +1 = 0 lösen. Mit der PQ-Formel erhalten wir x₁ = -1 und x₂ = -1.
• Wir erhalten damit ( x + 1 ) und noch einmal ( x + 1 ) für die Linearfaktoren.
• Die Produktdarstellung lautet damit: f(x) = ( x + 1 ) ( x + 1 ) = ( x + 1 )².
• Probe: ( x + 1 ) ( x + 1 ) = x² + 2x + 1.
• Alternativ kann hier auch mit den Binomischen Formeln gearbeitet werden.

Beispiel 3:

Eine Linearfaktorzerlegung von f(x) = 2x² + 7x -22 soll durchgeführt werden. Lösung:

• Bei den vorigen Beispielen hatten wir 1x², hier haben wir 2x².
• Den Koeffizienten "2" vor x² merken wir uns, denn diesen brauchen wir für die Produktdarstellung.
• Wir suchen mit der PQ-Formel die Nullstellen und erhalten x₁ = 2 und x₂ = -5,5.
• Die Linearfaktoren lauten ( x - 2 ) und ( x + 5,5 ).
• Produktdarstellung: Mit dem Koeffizienten erhalten wir f(x) = 2 ( x - 2 ) ( x + 5,5 ).
• Probe: 2 ( x - 2 ) ( x + 5,5 ) = 2x² + 7x - 22.

Beispiel 4:

Eine Zerlegung von f(x) = 3x³ - 10x² + 7x - 12 in Linearfaktoren soll durchgeführt werden. Lösung:

• Durch raten erhalten wir eine Nullstelle bei x = 3. Wir führen eine Polynomdivision durch:

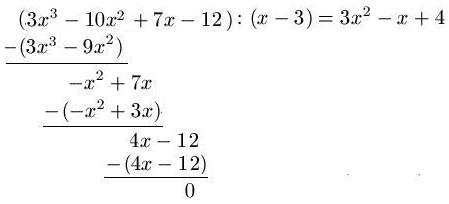
• Den Linearfaktor ( x - 3 ) konnten wir nun abspalten
• Das reduzierte Polynom 3x² - x + 4 bleibt übrig.
• Durch Einsatz der PQ-Formel sehen wir, dass 3x^₂ - x + 4 = 0 keine weiteren Nullstellen im reellen liefert.
• Damit konnten wir nur einen Linearfaktor abspalten. Dieser lautet ( x - 3 ).
• Wir erhalten: f(x) = ( x - 3 ) ( 3x² - x + 4 ).
• Probe: ( x - 3 ) ( 3x² - x + 4 ) = 3x³ - 10x² + 7x - 12.

Links:

• Linearfaktorzerlegung Aufgaben / Übungen
• Zur Mathematik-Übersicht