Die Raute der Mathematik lernst du hier kennen. Du bekommst zunächst eine schnelle Übersicht über die Raute. Im Anschluss sehen wir uns Beispiele und Formeln zu Umfang, Flächeninhalt und Winkeln an. Den Unterschied einer Raute zu einem Rechteck oder Quadrat sehen wir uns ebenfalls an.
Definition: Ein Raute ist ein Viereck mit vier gleich langen Seiten.
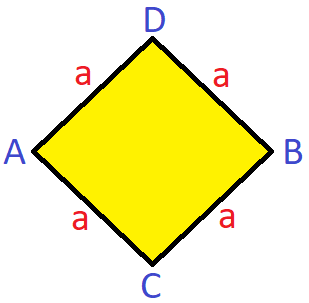
Die Eigenschaften einer Raute und Formeln für die Berechnung sehen wir uns mit entsprechenden Beispielen an.
Raute Eigenschaften
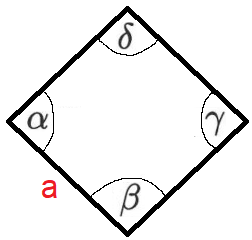
Zu den Eigenschaften einer Raute gehören vier gleich lange Seiten, vier Eckpunkte (A, B, C und D) sowie vier Winkel (Alpha, Beta, Gamma und Delta). Die gegenüberliegenden Winkel sind gleich groß, sprich Alpha und Gamma sind gleich groß und Beta und Delta sind ebenfalls gleich groß.
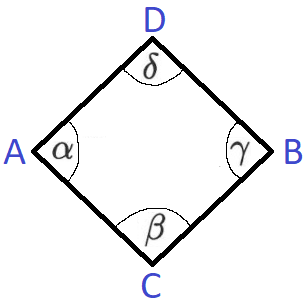
Die Winkel Alpha, Beta, Delta und Gamma ergeben zusammen eine Summe von 360 Grad. Die Winkel Alpha und Beta ergeben zusammen 180 Grad, ebenso ergeben die Winkel Gamma und Delta 180 Grad.
Diagonalen der Raute:
In eine Raute können zwei Diagonalen eingezeichnet werden. Dabei werden die gegenüberliegenden Eckpunkte verbunden. Die Diagonalen werden mit "e" und "f" bezeichnet. Die Diagonalen stehen senkrecht aufeinander und halbieren die Innenwinkel.
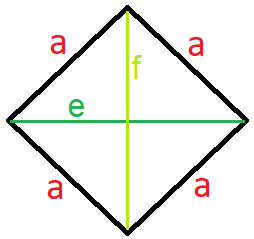
Mit dem Flächeninhalt und Umfang der Raute befassen wir uns als nächstes.
Raute Flächeninhalt: Formel mit Beispiel
Der Flächeninhalt einer Raute kann auf verschiedene Art und Weisen berechnet werden. Die Fläche kann aus den Diagonalen berechnet werden oder über Seitenlänge und Winkel Alpha. Die Formeln für den Flächeninhalt einer Raute lauten:

Flächeninhalt Raute über Diagonale Beispiel:
Die Diagonalen sind 3 Meter und 4 Meter lang. Wie groß ist die Fläche?

Um den Flächeninhalt zu berechnen multiplizieren wir die Länge der beiden Diagonalen miteinander und teilen durch 2.
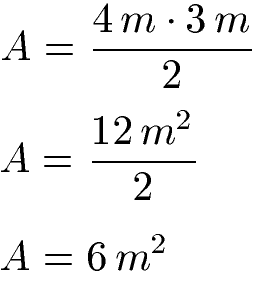
Flächeninhalt Raute über Winkel Beispiel:
Der Flächeninhalt der Raute kann über eine Seitenlänge und den Winkel Alpha berechnet werden.
Als Beispiel wird eine Seitenlänge von 4 Metern angenommen und der Winkel Alpha sei 70 Grad groß. Wie groß ist der Flächeninhalt? Als Lösung setzen wir die 4 Meter in die Formel ein und quadrieren sie. Den Winkel von 70 Grad rechnen wir mit dem Taschenrechner aus. Der Taschenrechner muss dabei auf DEG gestellt werden, sonst wird ein falsches Ergebnis berechnet.

Raute Umfang: Formel mit Beispiel
Der Umfang der Raute ist das Vierfache einer Seitenlänge. Da alle Seiten gleich lang sind, wird die gleiche Variable (a) an alle vier Seiten geschrieben.
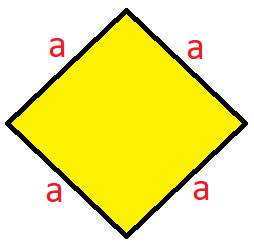
Die Formel um den Umfang einer Raute zu berechnen lautet:
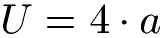
Ist eine Seite einer Raute 3 Meter langt ergibt sich ein Rautenumfang von 12 Metern.
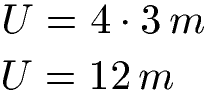
Winkel bei einer Raute
Bei einer Raute werden vier Innenwinkel angegeben. Diese Innenwinkel werden mit Alpha, Beta, Gamma und Delta bezeichnet.

Die Winkel Alpha und Gamma sind gleich groß, ebenso sind Beta und Delta gleich groß. Die benachbarten Winkel ergeben zusammen 180 Grad: Alpha und Beta ergeben zusammen 180 Grad, ebenso sind Beta und Delta zusammen 180 Grad. Alle vier Innenwinkel ergeben zusammen 360 Grad.

Beispiel Winkel bei Raute:
Der Winkel Alpha sei 80 Grad groß. Wie groß sind die anderen Winkel? Lösung: Alpha und Gamma sind gleich groß, daher ist auch Gamma 80 Grad. Die Winkel nebeneinander ergeben 180 zusammen, daher ist Beta 100 Grad. Beta und Delta sind gleich groß, daher ist Delta ebenso 100 Grad.
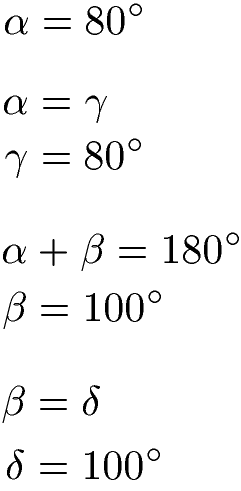
Raute: Vergleich zu Quadrat und Rechteck
Ein Quadrat ist eine Raute. Genauer gesagt ist ein Quadrat eine spezielle Raute. Die Besonderheit eines Quadrates besteht darin, dass alle 4 Winkel 90 Grad groß sind. Bei einer Raute können alle 4 Innenwinkel 90 Grad groß sein, müssen dies aber nicht.

Ein Rechteck ist eine Raute. Genauer gesagt ist ein Rechteck eine spezielle Raute. Die Besonderheit eines Rechtecks besteht darin, dass alle 4 Winkel 90 Grad groß sind. Bei einer Raute können alle 4 Innenwinkel 90 Grad groß sein, müssen dies aber nicht.

Weitere Links:
402 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige: