Verzinsung

Mit der Verzinsung ( von Guthaben ) befassen wir uns in diesem Artikel. Dabei liefern wir euch benötigtes Grundwissen sowie passende Formeln zur Berechnung, Beispiele inklusive. Dieser Artikel gehört zum Bereich Mathematik.

Die Verzinsung ist eine Anwendung der Prozentrechnung / Zinsrechnung. Solltet ihr von der Prozentrechnung noch nichts verstehen, empfiehlt es sich, diese erst einmal in unserem Artikel zur Prozentrechnung nachzulesen. Zwei weitere Punkte sollten euch zu dem klar sein, um mit der Zinsrechnung umgehen zu können.

Verzinsung für ein Jahr

Mit der Verzinsung für ein Jahr befassen wir uns in diesem Abschnitt: In der Zinsrechnung interessiert man sich oftmals dafür, wie viel Zinsen man für sein Erspartes nach einem Jahr erhält. Dies kann man mit der Formel zur Berechnung der Jahreszinsen ermitteln. Die Verzinsung für ein Jahr berechnet sich nach der folgenden Formel:

Dabei sind:

• "Z" die anfallenden Zinsen
• "p" der Zinssatz
• "K" das Kapital

Beispiel:

Auf einem Sparbuch werden 1200 Euro für einen Zeitraum von einem Jahr mit 3 Prozent verzinst. Wie viel Zinsen erhält der Inhaber des Sparbuchs nach einem Jahr?

Lösung: Dem Text entnehmen wir, dass K = 1200 Euro und p = 3 ist. Dies setzen wir in die eben genannte Formel ein.

Mit Hilfe dieser Formel zur Verzinsung haben wir nun ermittelt, dass die Zinsen für 1 Jahr 36 Euro betragen.

Verzinsung ( Monatszinsen )

Mit der Verzinsung von Monatszinsen befassen wir uns in diesem Artikel: Legt man sein Geld nicht für ein ganzes Jahr, sondern nur für 5 Monate fest, so erhält man natürlich weniger Zinsen für sein Guthaben, als für ein komplettes Jahr. Da ein Jahr 12 Monate hat, multipliziert man das Ergebnis aus der Verzinsung mit der Anzahl der Monate und dividiert durch 12. Die Formel sieht somit wie folgt aus:

Dabei sind:

• "Z" die anfallenden Zinsen
• "p" der Zinssatz
• "K" das Kapital
• "m" die Anzahl der Monate

Beispiel:

Zum besseren Verständnis ein weiteres Beispiel, um den Einsatz der Formel zu Verzinsung zu zeigen: Ein Guthaben von 18000 Euro wird für einen Zeitraum von 7 Monaten und einem Zinssatz von 4% festgelegt. Wie viel Zinsen fallen an?

Lösung: Dem Text entnehmen wir, dass K = 18000 Euro, p = 4 und m = 7 ist. Diese Angaben setzen wir in die Formel ein und berechnen die Zinsen.

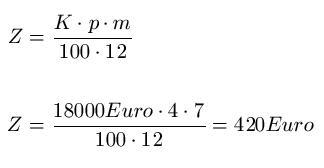
Tipp: Ihr solltet beim Rechnen mit dem Taschenrechner um den Nenner eine Klammer setzen, sonst multipliziert der Taschenrechner eventuell das Ergebnis mit 12, statt zu dividieren.

Verzinsung für Tageszinsen

Nach den Jahreszinsen und Monatszinsen fehlen noch die Tageszinsen und die entsprechde Formel zur Verzinsung. Dabei gilt folgendes zu beachten: In Deutschland rechnen die Banken mit 360 Tagen für ein Jahr. Dies muss sich natürlich auch in den Formeln der Zinsrechnung wieder spiegeln. Die Tageszinsen berechnen sich wie folgt:

Dabei sind:

• "Z" die anfallenden Zinsen
• "p" der Zinssatz
• "K" das Kapital
• "t" die Anzahl der Tage

Beispiel:

Ein Guthaben von 7600 Euro wird für 120 Tage zu einem Zinssatz von 5 Prozent festgelegt. Wie viel Zinsen fallen für den angegebenen Zeitraum an?

Lösung: Wir entnehmen dem Text, dass K = 7600 Euro, p = 5 und t = 120 ist. Diese Informationen setzen wir in die Formel ein und berechnen die Zinsen.

Links:

• Zur Mathematik-Übersicht