Wurzelziehen

Das Wurzelziehen - in einigen Fällen auch Radizieren genannt - erklären wir in diesem Artikel. Dabei erklären wir euch, wofür man das Wurzelziehen benötigt und liefern euch einige mathematische Gesetze sowie passende Beispiele.

Wofür benötigt man das Wurzelziehen überhaupt? Die Grundüberlegung: Welche Zahl muss man mit einem vorgegebenen Exponenten potenzieren, um eine vorgegebene Zahl zu erhalten. Diese Überlegung führt zu einer Umkehrung des Potenzierens, welches von uns im Folgenden als "Wurzelziehen" bezeichnet wird.

Beginnen wir mit der allgemeinen Darstellung. Diese sieht wie folgt aus:

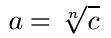
Dabei heißen "n" der Wurzelexponent, c der Radikand und a der Wurzelwert. Wurzeln mit dem Wurzelexponenten 2 heißen Quadratwurzeln. Wird bei einem Wurzelausdruck kein Wurzelexponent angegeben, ist dieser automatisch 2. Neben den Variablen a, n und c seht ihr in dieser Darstellung auch schon das Zeichen für die Wurzel.

Beispiele zum Wurzelziehen

Wir bereits erwähnt, ist das Radizieren die Umkehrung des Potenzierens. Mit diesem Wissen gehen wir nun an eine Reihe an Beispielen ran:

Hinweis: Es gibt nur wenige Zahlen, bei denen das Wurzelziehen so einfach ist. Dies sind die Zahlen 1 ,4, 9, 16, 25, 36 etc. , da beim ziehen aus diesen Wurzeln eine natürliche Zahl raus kommt. Bei komplizierteren Aufgaben empfiehlt sich der Einsatz eines Taschenrechners. Darüber hinaus ist ein wenig Übung notwendig, um diese Art des Rechnens zu erlernen.

Wurzelgesetze

Zur Berechnung von Wurzelausdrücken könnten weitere mathematische Formeln eingesetzt werden. Diese Formeln liefern wir euch im nun Folgenden zusammen mit Beispielen und werden als Wurzelgesetze bezeichnet.

In der Praxis müsst ihr nun erkennen, ob ihr eine der Formeln anwenden könnt. Seht euch dazu die euch gegebene Aufgabe genau an. Liegt eine Multiplikation zweier Wurzeln vor, dann verwendet das oberste der Gesetze. Selbige Vorgehensweise gilt auch für die anderen Gesetze. Um schnell die Wurzel ziehen zu können, lernt am Besten die Gesetze auswendig. Wer dies nicht möchte, sollte eine passende Formelsammlung stets zur Hand haben.

Weitere Links:

• Zur Mathematik-Übersicht