In diesem Artikel befassen wir uns mit dem Doppler-Effekt. Dabei wird erklärt, was man unter dem Doppler-Effekt versteht und wo dieser auftritt. Wir sehen uns die Formeln an, es werden Beispiele mit Zahlen vorgerechnet und Anwendungen für den Doppler-Effekt vorgestellt. Dieser Artikel gehört zu unserem Bereich Physik.
Der eine oder andere kann sich daran vielleicht erinnern: Ihr steht am Straßenrand und ein Krankenwagen fährt mit eingeschalteter Sirene an euch vorbei. Dann ist euch vielleicht aufgefallen, dass sich die Tonlage ändert? Nähert sich der Krankenwagen euch dann ist der Ton höher, entfernt er sich dann wieder von euch wird der Ton tiefer. Würde der Krankenwagen neben euch stehenbleiben, würdet ihr keine Veränderung der Tonhöhe bemerken. Genau dies bezeichnet man als Doppler-Effekt. Er tritt jedoch nicht nur bei Schallwellen auf, sondern auch bei Lichtwellen. Dies sehen wir uns bei den Anwendungen auch noch näher an.
Zuvor werfen wir jedoch einen Blick auf die Formeln und nehmen dazu auch Beispiele, in welche Zahlen und Einheiten eingesetzt werden. Denn daran mangelt es sehr häufig in Büchern und auch auf Internet-Seiten. Auch werde ich die jeweilige Formel mit Beispiel einzeln angeben und nicht wie das gerne gemacht wird diese mit +/- zusammenschreiben.
Doppler-Effekt: Formeln und Beispiele
Viele haben Probleme Aufgaben für den Doppler-Effekt zu berechnen. Aus diesem Grund sehen wir uns nun die Formeln für entsprechende Beispiele an. Entscheidend für die Beispiele ist, ob sich der Sender oder der Empfänger bewegt und ob diese sich aufeinander zubewegen oder von einander wegbewegen.
Für die Formeln gelten folgende Angaben:
- "fE" ist die Frequenz, die beim Empfänger ankommt in Hertz
- "fS" ist die Frequenz, die vom Sender abgegeben wird in Hertz
- "v" ist die Relativgeschwindigkeit zwischen Sender und Empfänger in Meter pro Sekunde
- "c" ist die Ausbreitungsgeschwindigkeit der Wellen (in unseren Beispielen Schallgeschwindigkeit) in Meter pro Sekunde
Formel Nr. 1: Sender bewegt sich, Empfänger steht still, Sender bewegt sich auf Empfänger zu
Beispiel 1: Ein Krankenwagen hat seine Sirene mit einer Hauptfrequenz von 1500 Hz an und fährt mit 30 Meter pro Sekunde über die Straße. Du stehst am Straßenrand, der Krankenwagen fährt auf dich zu. Welche Frequenz hörst du?
Lösung: In diesem Beispiel bewegt sich der Sender auf den Empfänger zu. Wir nehmen daher die folgende Formel mit einem minus im Nenner und setzen die Angaben ein. Dabei ist fS = 1500 Hz, v = 30 m/s und die Schallgeschwindigkeit c = 343 m/s.
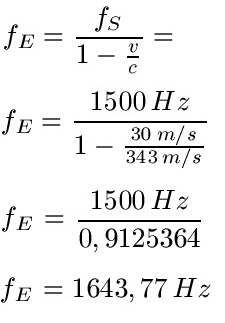
Formel Nr. 2: Sender bewegt sich, Empfänger steht still, Sender bewegt sich von Empfänger weg
Beispiel 2: Ein Krankenwagen hat seine Sirene mit einer Hauptfrequenz von 1500 Hz an und fährt mit 30 Meter pro Sekunde über die Stra0e. Du stehst am Straßenrand, der Krankenwagen ist an dir vorbeigefahren und fährt weiter von dir weg. Welche Frequenz hörst du?
Lösung: In diesem Beispiel bewegt sich der Sender vom Empfänger weg (im Gegensatz zum vorherigen Beispiel). Wir nehmen daher die Formel mit einem plus im Nenner und setzen die Angaben ein. Dabei ist fS = 1500 Hz, v = 30 m/s und die Schallgeschwindigkeit c = 343 m/s.
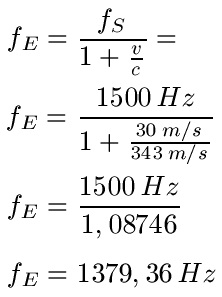
Formel Nr. 3: Sender steht still, Empfänger bewegt sich, bewegen sich aufeinander zu
Beispiel Nr.3: Jetzt sieht es umgekehrt aus. Diesmal steht der Sender still und der Empfänger bewegt sich. Der Empfänger bewegt sich dabei auf den Sender zu. Die Quelle gibt eine Frequenz von 4000 Hz ab, der Empfänger bewegt sich mit 5 m/s auf den Sender zu.
Lösung: Wir benötigen nun die Formel für einen stehenden Sender und einen bewegenden Empfänger und ein aufeinander zubewegen. Dabei ist "fS" = 4000 Hz und v = 5 m/s, die Schallgeschwindigkeit sei wieder c = 343 m/s.
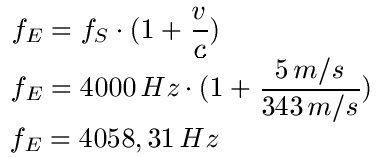
Formel Nr. 4: Sender steht still, Empfänger bewegt sich, bewegen sich voneinander weg
Beispiel 4: Fehlt noch die vierte Option. Der Sender steht still, der Empfänger bewegt sich und sie bewegen sich voneinander weg. Die Quelle gibt eine Frequenz von 4000 Hz ab, der Empfänger bewegt sich mit 5 m/s vom Sender weg.
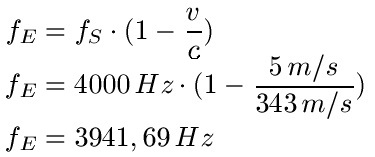
Doppler-Effekt Anwendungen
Wir haben uns damit befasst, was der Doppler-Effekt ist, wir haben uns Formeln und Beispiele angesehen. Bleibt also noch die Frage: Wozu kann man den Doppler-Effekt gebrauchen? Sehen wir uns einmal ein paar Beispiele an (es gibt Unmengen mehr Anwendungen, aber dies würde den Artikel hier sprengen):
- Radar: Die erste Anwendung des Doppler-Effekts die wir uns hier ansehen möchten ist das Doppler-Radar. Dabei berechnet man die Annäherungsgeschwindigkeit eines Objekts aus der gemessenen Frequenzänderung zwischen gesendetem und zurückgeworfenem Signal.
- Medizin: In der Medizintechnik wird der akustische Doppler-Effekt bei Ultraschalluntersuchungen ausgenutzt, um die Geschwindigkeit des Blutstroms darzustellen und diesen zu messen.
- Astrophysik: Auch in der Astrophysik findet der Doppler-Effekt eine Anwendung. Hier spricht man dann vom relativistischen Doppler-Effekt, der basiert jedoch nicht auf Schallwellen sondern ist optisch, daher wird er manchmal auch als optischer Doppler-Effekt bezeichnet. Mit diesem kann man Rückschlüsse auf Bewegungen zum Beispiel von Galaxien durchführen.
Links:
1797 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige:
