Linearfaktorzerlegung Lösung

In diesem Artikel findet ihr die Lösungen der Aufgaben bzw. Übungen zur Linearfaktorzerlegung / Produktdarstellung. Löst diese Aufgaben zunächst selbst und seht erst im Anschluss in die Lösungen. Bei Problemen findet ihr Hilfe im Infoartikel. Dieser Artikel gehört zu unserem Bereich Mathematik.

• Linearfaktorzerlegung Artikel
• Linearfaktorzerlegung Aufgaben

Lösung Aufgabe 1: Linearfaktorzerlegung / Produktdarstellung

Führe für die folgenden Aufgaben eine Linearfaktorzerlegung / Produktdarstellung durch:

Beispiel 1:

Gegeben sei f(x) = x² - 2x - 8.  Es soll eine Zerlegung in Linearfaktoren durchgeführt werden. Lösung:

• Wir müssen die Gleichung x² - 2x - 8 = 0 lösen. Mit der PQ-Formel erhalten wir x₁= 4  und x₂ = -2.
• Die Linearfaktoren lauten damit ( x - 4 ) und ( x + 2 ).
• Wir erhalten damit f(x) = ( x - 4 ) ( x + 2 ) für die Produktdarstellung
• Probe: ( x - 4 ) ( x + 2 ) = x² - 2x - 8.

Beispiel 2:

Geben sei f(x) = x² + 2x + 1. Eine Zerlegung in Linearfaktoren soll durchgeführt werden. Lösung:

• Wir müssen  x² + 2x +1 = 0 lösen. Mit der PQ-Formel erhalten wir x₁ = -1 und x₂ = -1.
• Wir erhalten damit ( x + 1 ) und noch einmal ( x + 1 ) für die Linearfaktoren.
• Die Produktdarstellung lautet damit: f(x) = ( x + 1 ) ( x + 1 ) = ( x + 1 )².
• Probe: ( x + 1 ) ( x + 1 ) = x² + 2x + 1.
• Alternativ kann hier auch mit den Binomischen Formeln gearbeitet werden.

Beispiel 3:

Eine Linearfaktorzerlegung von f(x) = 2x² + 7x -22 soll durchgeführt werden.  Lösung:

• Bei den vorigen Beispielen hatten wir 1x², hier haben wir 2x².
• Den Koeffizienten "2" vor x² merken wir uns, denn diesen brauchen wir für die Produktdarstellung.
• Wir suchen mit der PQ-Formel die Nullstellen und erhalten x₁ = 2 und x₂ = -5,5.
• Die Linearfaktoren lauten ( x - 2 ) und ( x + 5,5 ).
• Produktdarstellung: Mit dem Koeffizienten erhalten wir f(x) = 2 ( x - 2 ) ( x + 5,5 ).
• Probe: 2 ( x - 2 ) ( x + 5,5 ) = 2x² + 7x - 22.

Beispiel 4:

Eine Zerlegung von f(x) = 3x³ - 10x² + 7x - 12 in Linearfaktoren soll durchgeführt werden. Lösung:

• Durch raten erhalten wir eine Nullstelle bei x = 3. Wir führen eine Polynomdivision durch:

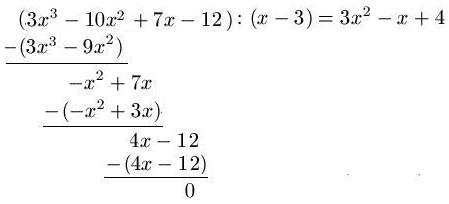
• Den Linearfaktor ( x - 3 ) konnten wir nun abspalten
• Das reduzierte Polynom 3x² - x + 4 bleibt übrig.
• Durch Einsatz der PQ-Formel sehen wir, dass 3x^₂ - x + 4 = 0 keine weiteren Nullstellen im reellen liefert.
• Damit konnten wir nur einen Linearfaktor abspalten. Dieser lautet ( x - 3 ).
• Wir erhalten: f(x) = ( x - 3 ) ( 3x² - x + 4 ).
• Probe: ( x - 3 ) ( 3x² - x + 4 ) = 3x³ - 10x² + 7x - 12.

Links:

• Zur Mathematik-Übersicht