Pole und Nullstellen Lösungen

In diesem Abschnitt findet ihr nun die Lösungen der Übungen und Aufgaben zu Polen und Nullstellen. Rechnet diese Aufgaben zunächst selbst durch und schaut danach erst in unsere Lösungen.

• Artikel: Pole und Nullstellen
• Aufgabenstellung: Pole und Nullstellen

Lösungen Aufgabe 1: Beantworte die Fragen
1a) Eine Nullstelle einer Funktion ist die Abszisse / x-Koordinate eines Schnittpunktes des Funktionsgraphen mit der x-Achse. Eine gebrochenrationale Funktion besitzt überall dort eine Nullstellen x₀, wo das Zählerpolynom g(x) den Wert Null, das Nennerpolynom h(x) einen von Null verschiedenen Wert annimmt.

1b) Polstellen einer gebrochenrationalen Funktion sind demnach Stellen, in denen das Nennerpolynom h(x) verschwindet, das Zählerpolynom g(x) jedoch einen von Null verschiedenen Wert annimmt.

1c)

• Nullstellen und Pole geben Hinweise darauf, wie eine Funktion ( zeichnerisch ) aussieht.
• Aus der Bruchrechnung wisst ihr hoffentlich noch, dass durch Null nicht dividiert werden darf. Ihr dürft somit keine Zahlen in die Gleichung einsetzen, bei der eine Division durch Null erfolgen würde.
• Eine Anwendung: Die Lage der Pole und Nullstellen liefert in der Regelungstechnik Informationen zum Verhalten dynamischer Systeme. Mit der Pol-Nullstellen-Verteilung kann zu dem Reglersynthese mittels Wurzelortskurve betrieben werden.

Lösungen Aufgabe 2: Berechne die Pole und Nullstellen

Hinweis: Ihr müsst mit der PQ-Formel richtig umgehen können. Bei Problemen mit dieser hilft unser Artikel PQ-Formel.

2a) n1=-8 ; p1=+3

2b) n1=-2; p1=0

2c) n1=2; n2=-3; p1=-4

2d) n1=-0,23; n2=-8,77; p1=0,56; p2=-3,56

2e) n1=0; p1=-1; p2=-2

2f)

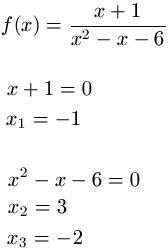
2g)

2h)

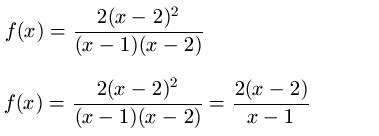
Links:

• Zur Mathematik Übersicht