Zehnerpotenzen lernst du in diesem Artikel kennen. Du lernst wie man eine Zehnerpotenz berechnet, welche Namen Zehnerpotenzen haben und wie sie für kleine und große Zahlen verwendet werden können. Außerdem geht es um das Rechnen mit Zehnerpotenzen bei Addition, Subtraktion, Multiplikation und Division. Abgetrennte Zehnerpotenzen und Stufenzahlen werden ebenso kurz behandelt. Die Inhalte liegen als Text und als Video vor.
Zehnerpotenzen sind Potenzen bei denen die Basis 10 ist. Zehnerpotenzen helfen dabei sehr große und sehr kleine Zahlen in der Mathematik darzustellen. Für die Darstellung großer Zahlen wird ein positiver Exponent verwendet. Der Potenzwert hat so viele Nullen wie der Exponent groß ist. Bei 3 als Exponent hat der Potenzwert 3 Nullen.

Im Normalfall werden bei Zehnerpotenzen ganze Zahlen verwendet. Ganze Zahlen sind ... -3, -2, -1, 0, 1, 2, 3, ... Für große Zahlen wird ein positiver Exponent verwendet, für sehr kleine Zahlen hingegen ist die Hochzahl negativ. Der Exponent gibt in diesem Fall an wie viele Stellen wir hier dem Komma haben, sprich an welcher Stelle die 1 hinter dem Komma steht.

Zehnerpotenzen werden alternativ auch als 10er-Potenzen oder Stufenzahlen bezeichnet.
Zehnerpotenzen Beispiele berechnen
Zehnerpotenzen können addiert, subtrahiert, multipliziert und dividiert werden. Bevor wir jedoch diese Grundrechenarten verwenden können, solltest du eine Potenz selbst erst einmal ausrechnen können.
Haben wir eine natürliche Zahl (1, 2, 3, 4 und so weiter) als Hochzahl wird die 10 so oft mit sich selbst multipliziert wie der Exponent dies vorgibt. Sieh dir die drei Beispiele zu Zehnerpotenzen mit natürlicher Hochzahl an:
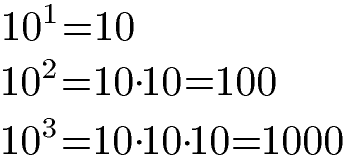
Eine Zehnerpotenz mit negativem Exponenten dient dazu sehr kleine Zahlen darzustellen. Es handelt sich dabei um Dezimalzahlen (Kommazahlen). Der Exponent gibt dabei vor an welcher Stelle hinter dem Komma die 1 steht. Eine -3 als Exponent sagt, dass die 1 an der 3. Stelle nach dem Komma steht.
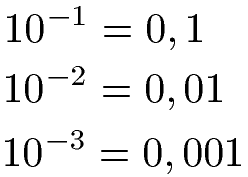
Zehnerpotenz mit negativem Exponenten berechnen:
Wie kann man eine Zehnerpotenz mit negativem Exponenten berechnen? Dazu sollte man sich an das Rechnen mit Potenzen erinnern. Eine Potenz mit einem negativen Exponenten kann durch einen Bruch in eine Potenz mit einem positiven Exponenten umgewandelt werden. Die allgemeine Schreibweise lautet:
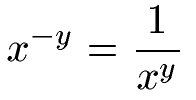
Als Beispiel dienen zwei Potenzen mit negativer Hochzahl. Die Umwandlung erfolgt über einen Bruch mit einer 1 im Zähler. Im Nenner findet sich erneut die Potenz wieder, jedoch mit umgekehrtem Vorzeichen.
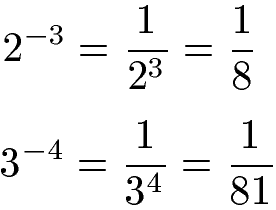
Es spielt dabei keine Rolle, ob es sich um eine Potenz mit beliebiger Basis oder um eine Potenz mit Basis 10 (Zehnerpotenz) handelt.
Zehnerpotenzen und Stufenzahlen
Zehnerpotenzen werden manchmal auch als Stufenzahlen bezeichnet. Um dies zu verstehen, schreiben wir eine Zahl zunächst in eine Stellenwerttafel. Dabei handelt es sich um eine Tabelle bei denen die Zahl in einzelne Stellen zerlegt wird. Achte dabei auf die Zehnerpotenzen (grün markiert).

Die 2 steht dabei auf der Stelle 103 oder die 8 auf der Stelle bei 100. Das Beispiel mit 2538 kann aus diesem Grund als eine Summe aus Zehnerpotenzen dargestellt werden.

Werden die einzelnen Zehnerpotenzen ausgerechnet entsteht dabei wieder die Zahl 2538. Beim Rechnen mit Zehnerpotenzen (Siehe weiter unten) werden wir dies ausführlich behandeln.
Zehnerpotenzen Tabelle: Namen und Vorsilben
Eine Tabelle zu Zehnerpotenzen hilft dabei eine Übersicht über die Potenzen mit der Basis 10 zu bekommen. Die nächste Tabelle gibt dabei die Zehnerpotenzen an, welcher Zahl diese ausgerechnet entsprichst sowie den Namen und die Vorsilbe.
Tabelle nach rechts scrollbar
| Zehnerpotenz | Zahl | Name | Vorsilbe |
| 100 | 1 | Eins | Eins |
| 101 | 10 | Zehn | Deka |
| 102 | 100 | Hundert | Hekto |
| 103 | 1000 | Tausend | Kilo |
| 104 | 10000 | Zehntausend | |
| 105 | 100000 | Hunderttausend | |
| 106 | 1000000 | Million | Mega |
| 10-1 | 0,1 | Zehntel | Dezi |
| 10-2 | 0,01 | Hundertstel | Zenti |
| 10-3 | 0,001 | Tausendstel | Milli |
| 10-4 | 0,0001 | Zehntausendstel | |
| 10-5 | 0,00001 | Hunderttausendstel | |
| 10-6 | 0,000001 | Millionstel | Mikro |
In den Naturwissenschaften (Mathematik, Physik, Biologie oder Chemie) werden sehr häufig Zehnerpotenzen verwendet. Hier wird von wissenschaftlicher Schreibweise oder technischer Schreibweise gesprochen. Bei kleinen Entfernungen wird zum Beispiel nicht von 0,000001 Metern gesprochen, sondern dies kurz mit 10-6 m oder 1 Mikrometer (= 1 µm) beschrieben.
Bei der Darstellung sehr kleiner oder sehr große Zahlen fällt in einigen Fällen der Begriffe "abgetrennte Zehnerpotenzen" bei denen man die eben gezeigte Tabelle einsetzt. Daher sehen wir uns vor dem weiteren Rechnen mit Zehnerpotenzen erst einmal die abgetrennten Zehnerpotenzen an.
Abgetrennte Zehnerpotenzen
In naturwissenschaftlichen und technischen Zusammenhängen tauchen sehr oft extrem große oder extrem kleine Zahlen auf. Der Einsatz von abgetrennten Zehnerpotenzen hilft, die Darstellung großer und kleiner Zahlen deutlich zu verkürzen.
Abgetrennte Zehnerpotenzen bestehen aus einer Zehnerpotenz. Diese Zehnerpotenz wird mit einer weiteren Zahl multipliziert, welche vor oder nach der Zehnerpotenz geschrieben wird (meistens davor). Selbstverständlich kann diese Zehnerpotenz ausgerechnet werden.

Abgetrennte Zehnerpotenzen werden auch zur Darstellung sehr kleiner Zahlen verwendet. Auch hier wird eine Zehnerpotenz verwendet, in diesem Fall mit einem negativen Exponenten. Die Zehnerpotenz wird ebenfalls mit einer Zahl multipliziert. Natürlich kann auch dies in Form einer Dezimalzahl (Kommazahl) ausgerechnet werden.
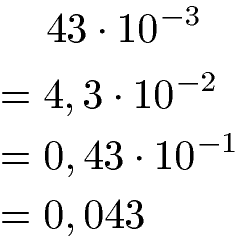
Hinweis: Werden Potenzausdrücke berechnet wird von der Rechenreihenfolge her eigentlich zuerst die Potenz berechnet und im Anschluss die Multiplikation mit der Zahl davor. Wird jedoch eine abgetrennte Zehnerpotenz umgerechnet kann diese auch Stück für Stück durch Versetzen vom Komma oder Nullen umgewandelt werden.
Zehnerpotenzen addieren und subtrahieren
Zehnerpotenzen können addiert und subtrahiert werden. Dazu werden die Zehnerpotenzen zunächst in Zahlen ohne Potenzschreibweise umgewandelt. Zum besseren Verständnis sehen wir uns dazu ein Beispiel mit Zehnerpotenzen mit Addition und Subtraktion an.

In der Mathematik und für Potenzen gilt für die Reihenfolge der Berechnung folgende Regel: Zuerst werden Potenzen berechnet und im Anschluss Punkt vor Strich. Die erste Potenz habe ich daher direkt mit dieser Regel umgerechnet: Zuerst die Potenz 102 berechnen und danach mit 3 multiplizieren. Viele Menschen tun sich jedoch mit dieser Berechnung schwer, insbesondere wenn der Exponent negativ ist. Daher habe ich für die Umformung der beiden anderen Zahlen das Verfahren der abgetrennten Zehnerpotenzen von weiter oben eingesetzt.

Nach Umrechnung aller Potenzen auf Zahlen können diese im Anschluss subtrahiert und addiert werden.

Zehnerpotenzen multiplizieren und dividieren
Bei der Multiplikation und Division von Zehnerpotenzen werden zunächst die Potenzen vollständig berechnet. Dazu wird die Zehnerpotenz ausgerechnet und im Anschluss mit der Zahl davor multipliziert oder dividiert.
Das nächste Beispiel zeigt die Multiplikation von Zehnerpotenzen im Zähler eines Bruchs. Zur Erinnerung: Ein Bruch ist nichts anderes als die Division von zwei Zahlen, daher liegt hier ebenfalls eine Division von Zehnerpotenzen vor. Zunächst rechnen wir die Potenzen aus und berechnen Zähler und Nenner. Im Anschluss wird der Bruch (= die Division) ausgerechnet.

Weitere Links:
403 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige:




