Potenzen ▷ Erklärung und Beispiele

Was Potenzen sind und wo sich Basis und Exponent befinden, lernst du in diesem Artikel. Außerdem bekommst du Beispiele zum Rechnen mit Potenzen und lernst die Potenzgesetze kennen. Zehnerpotenzen und die Stufenform von Potenzen werden ebenfalls besprochen. Die Inhalte liegen als Text und als Video vor.

Die Potenz ist eine Abkürzung für die Multiplikation gleicher Zahlen.

Eine Potenz besteht aus zwei Teilen: Basis und Exponent. Die Basis wird dabei auch Grundzahl genannt. Die kleine Zahl oben wird Exponent oder Hochzahl genannt. Basis und Exponent werden zusammen als Potenz bezeichnet.

Eine Potenz wird berechnet, indem die Basis so oft mit sich selbst multipliziert wird wie der Exponent dies vorgibt. Ist die Basis 2 und der Exponent 3, so wird die 2 insgesamt 3 Mal geschrieben und miteinander multipliziert. Das Ergebnis einer Multiplikation wird Produkt genannt. Da es sich hier jedoch um das Berechnen einer Potenz handelt, wird das Ergebnis auch als Potenzwert bezeichnet.

Eine Potenz mit der Basis 2 wird auch als Zweierpotenz bezeichnet. Eine Potenz mit der Basis 10 wird Zehnerpotenz genannt.

Potenzen berechnen

Die Zahl im Exponenten gibt an, wie oft die Basis als Faktor geschrieben werden muss. Bei 3 als Basis und 2 als Exponent wird die Zahl 3 insgesamt 2 Mal geschrieben. Bei 5 als Basis und 3 als Exponenten wird die Zahl 5 insgesamt 3 Mal geschrieben. Die Potenzwerte sind für diese Beispiele 9 und 125.

Zwei Sonderfälle tauchen beim Rechnen mit Potenzen auf. Ein sehr einfacher Fall liegt vor, wenn die Basis einer Potenz 0 ist. In diesem Fall ist der Potenzwert 0.

Ist der Exponent einer Potenz 0 so ist der Potenzwert 1.

Das Rechnen mit Potenzen sowie den Umgang und das Vereinfachen von Potenzen sehen wir uns in den nächsten Abschnitten an.

Potenzen in Termen und Gleichungen

Potenzen können in Termen und Gleichungen vorkommen. Die Reihenfolge bei der Berechnung ergibt sich aus den Rechenregeln der Mathematik. Mit dieser Priorität wird gerechnet:

1. Klammern zuerst berechnen
2. Potenzen berechnen
3. Punktrechnung (Multiplikation und Division)
4. Strichrechnung (Addition und Subtraktion)
5. Von links nach rechts

Merke: Potenzen werden vor Multiplikationen und Divisionen berechnet!

Beispiel: Potenzen bei Terme und Gleichungen:

Im nächsten Beispiel wird zuerst die Klammer berechnet. Direkt im Anschluss wird die Potenz ausgerechnet. Bei zwei Multiplikationen wird zunächst die Multiplikation weiter links berechnet. Als letzter Schritt wird die Addition durchgeführt.

Merke: Die Regel Punkt vor Strich wird nach der Berechnung der Potenz angewendet. Weitere Beispiele zum Rechnen mit Potenzen und der Priorität findest du unter Potenzen Vorrangregeln.

Vergleichen von Potenzen

Um Potenzen miteinander zu vergleichen, solltest du alle Potenzen ausrechnen. Die Potenzwerte - so nennt man das Ergebnis wenn eine Potenz ausgerechnet wird - können im Anschluss sehr einfach verglichen werden.

Im ersten Beispiel sollen die Potenzen 4³ und 5² mit einander verglichen werden. Dazu rechnen wir beide Potenzen aus und vergleichen im Anschluss 64 und 25. Da 64 größer ist als 25 können wir das Vergleichszeichen für größer (>) einfügen. Dies tun wir im Anschluss auch für die beiden Potenzen.

Als zweites Beispiel werden die Potenzen 8² und 4⁵ verglichen. Wir rechnen beide Potenzen aus und vergleichen die Potenzwerte miteinander. Da 64 kleiner ist als 1024 ist auch 8² kleiner als 4⁵.

Zehnerpotenzen und Stufenform

Zehnerpotenzen sind Potenzen mit der Zahl 10 als Basis. Die Zahl wird dabei so lange mit sich selbst multipliziert wie der Exponent dies vorgibt. Als Produkt bzw. Potenzwert entstehen Zahlen mit einer 1 am Anfang, gefolgt von Nullen.

Zahlen können mit der Hilfe einer Stellenwerttafel zerlegt werden. In der Grundschule wird dabei eine Zerlegung in Einer, Zehner, Hunderter, Tausender und mehr durchgeführt. Ab der 5. Klasse wird die Stellenwerttafel auch dazu eingesetzt eine Dezimalzahl in Stufenform zu bringen. Die Einerstelle entspricht dabei 10⁰, die Zehnerstelle 10¹ und so weiter.

Die Zahl 83549 aus der letzten Stellenwerttafel kann dabei auch in Form einer Addition aus Zehnerpotenzen geschrieben werden. Dies wird in der Mathematik manchmal als Stufenzahl beschrieben:

Potenzen mit negativer Basis oder negativem Exponenten

Bei Potenzen können auch negativen Zahlen vorkommen. Sowohl die Basis als auch der Exponent können dabei Minuszahlen sein. Liegt bei der Basis eine negative Zahl vor, muss auf das Vorzeichen des Potenzwertes geachtet werden.

Negative Basis, ungerader Exponent:

Ist der Exponent eine ungerade Zahl, ist das Ergebnis negativ. Eine ungerade Zahl ist dabei eine natürliche Zahl mit einer 1, 3, 5, 7 oder 9 auf der letzten Stelle. Für das nächste Beispiel haben wir mit der 3 einen ungeraden Exponenten und damit einen negativen Potenzwert.

Negative Basis, gerader Exponent:

Ist er Exponent hingegen eine gerade natürliche Zahl, ist das Ergebnis positiv. Eine gerade natürliche Zahl ist eine Zahl, die auf 0, 2, 4, 6 oder 8 endet. Im nächsten Beispiel liegt mit +4 eine gerade natürliche Zahl als Hochzahl vor. Daher ist das Ergebnis mit +81 positiv.

Negativer Exponent:

Ist der Exponent einer Potenz negativ kann die Potenz in einen Bruch umgewandelt werden. Durch die Umwandlung der Potenz in einen Bruch kann das Vorzeichen der Hochzahl umgedreht werden. Die allgemeine Schreibweise lautet:

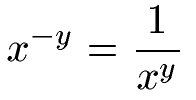
Als Beispiel zwei Potenzen mit negativem Exponenten. Die Umwandlung erfolgt über einen Bruch mit einer 1 im Zähler. Im Nenner findet sich erneut die Potenz wieder, jedoch mit umgekehrtem Vorzeichen.

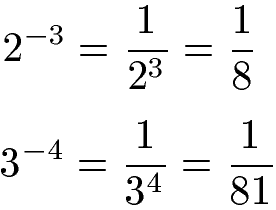
Vereinfachen von Potenzen

Potenzen können durch Einsatz von Potenzgesetzen vereinfacht werden. Die Potenzgesetze bzw. Potenzregeln beinhalten alle Grundrechenarten (Addition, Subtraktion, Multiplikation und Division). Außerdem dienen sie dazu Potenzen mit Wurzeln und Brüchen zu vereinfachen. Wir sehen uns gleich dazu einen Auszug an. Ausführlich behandele ich dies noch im Artikel und Video unter Potenzgesetze.

Bei den Potenzgesetzen tauchen Variablen (=Buchstaben) in der Basis und im Exponenten auf. Grundsätzlich gilt: Variablen sind Platzhalter für Zahlen. Für diese Variablen werden später Zahlen eingesetzt. Gleicher Buchstabe bedeutet gleiche Zahl. Potenzen können ebenso wie einfache Zahlen ausmultipliziert oder gleiche Variablen als Potenz zusammengefasst werden.

Mit diesem Wissen gehen wir nun an die Vereinfachung von Potenzen.

Potenzen addieren:

Bei gleicher Basis und gleichem Exponenten (=Hochzahlen) können zwei Potenzen einfach addiert werden. Dazu werden die Koeffizienten (hier a und b) einfach addiert während der restliche Teil unverändert bleibt. Die allgemeine Gleichung und zwei Beispiele zur Addition von Potenzen:

Weitere Beispiele und Erklärungen unter Potenzen addieren.

Potenzen subtrahieren:

Bei gleicher Basis und gleichem Exponenten (=Hochzahlen) können zwei Potenzen einfach subtrahiert werden. Dazu werden die Koeffizienten (hier a und b) einfach subtrahiert während der restliche Teil unverändert bleibt. Die allgemeine Gleichung und zwei Beispiele zur Subtraktion von Potenzen:

Weitere Beispiele und Erklärungen unter Potenzen subtrahieren.

Potenzen multiplizieren:

Potenzen mit gleicher Basis werden multipliziert, indem die Exponenten addiert werden und die Basis unverändert bleibt. Die allgemeine Schreibweise gefolgt von zwei Beispielen:

Weitere Beispiele zum Umgang mit gleichen bzw. unterschiedlichen Basen und Exponenten gibt es unter Potenzen multiplizieren.

Potenzen dividieren:

Potenzen mit gleicher Basis können dividiert werden, indem die Exponenten (Hochzahlen) subtrahiert werden während die Basis beibehalten wird. Die allgemeine Schreibweise und ein Beispiel:

Weitere Beispiele zum Umgang mit gleichen bzw. unterschiedlichen Basen und Exponenten gibt es unter Potenzen dividieren.

Basis und Exponent berechnen

Bei Potenzen können auch Variablen (Buchstaben) vorkommen. Eine Variable ist ein Platzhalter für eine Zahl, die später einmal eingesetzt werden kann.

Basis berechnen:

Ist bei einer Potenz die Basis unbekannt (x) so kann diese Basis mit einer Wurzel berechnet werden. Sehen wir uns ein einfaches Beispiel für nur positive Zahlen an.

Die Wurzelrechnung ist ein umfangreiches Gebiet der Mathematik. Beispiele und Erklärungen dazu findest du unter Wurzel (Wurzelrechnung).

Exponent berechnen:

Auch im Exponenten einer Potenz kann eine Variable vorkommen. Die Berechnung dieser Unbekannten erfolgt durch Einsatz des Logarithmus.

Die Logarithmusrechnung ist ein umfangreiches Gebiet der Mathematik. Beispiele und Erklärungen dazu findest du unter Logarithmus.

Quadratzahlen, Kubikzahlen und Zweierpotenzen

In diesem Abschnitt sehen wir uns weitere spezielle Potenzen an. Dazu zählen die Quadratzahlen, die Kubikzahlen und die Zweierpotenzen. Quadratzahlen sind dabei Potenzen mit dem Exponenten 2 und einer natürlichen Zahl als Basis. Mit anderen Worten: Eine natürliche Zahl wird mit sich selbst multipliziert. Die ersten Quadratzahlen lauten:

Kubikzahlen sind Potenzen mit dem Exponenten 3 und einer natürlichen Basis. Mit anderen Worten: Eine Kubikzahl entsteht indem eine natürliche Zahl zwei Mal mit sich selbst multipliziert wird. Die ersten Kubikzahlen sind diese:

Zweierpotenzen sind Potenzen mit der Basis 2. Es folgen einige Beispiele für Zweierpotenzen:

Links:

• Potentgesetze (Potenzregeln)
• Zehnerpotenzen
• Potenzen Vorrangregeln
• Übungen: Potenzen
• Mathematik-Übersicht