Gleichmäßig Beschleunigte Bewegung

Die gleichmäßig beschleunigte Bewegung wird in diesem Kapitel behandelt. Dabei erklären wir euch anhand von Beispielen, was es damit überhaupt auf sich hat. Selbstverständlich zeigen wir euch dabei auch die benötigen Formeln und liefern Übungen samt Lösungen, damit ihr mit diesem Gebiet fit werdet.

Im letzten Abschnitt haben wir die gleichförmigen Bewegung behandelt. Zur Erinnerung: Dabei handelt es sich um eine Bewegung eines Objektes, dass immer gleich schnell ist, sprich weder schneller noch langsamer wird. Bevor wir zur beschleunigten Bewegung kommen, gibt es ein paar ganz grundlegende Dinge aus der Mathematik, die ihr kennen solltet. Wenn ihr beim Lesen des folgenden Abschnitts erkennt, dass ihr mathematische Schwierigkeiten habt, dann lest bitte noch die Artikel unter den folgenden Links. Alle anderen können sich dies sparen:

• Mathematik: Punkt vor Strichrechnung
• Mathematik: Lineare Gleichungen
• Physik: Gleichförmige Bewegung

Die gleichmäßig beschleunigte Bewegung

Nun kümmern wir uns um die gleichmäßig beschleunigte Bewegung. Diese hat die folgenden Eigenschaften:

• Die Geschwindigkeit des Objektes ändert sich, wird entweder schneller oder langsamer
• Somit ist die Beschleunigung - meist mit "a" bezeichnet - ungleich Null
• Die Beschleunigung ist bei einer gleichmäßig beschleunigten Bewegung immer konstant

Also noch einmal: Die Beschleunigung ist immer gleich. Beispiel: a=5m/s². Dies bedeutet, dass das Objekt mit 5m/s² beschleunigt. Während der Bewegung ändert sich "a" nicht, sonst wäre die Beschleunigung nicht mehr gleichmäßig.

Gleichmäßig beschleunigte Bewegung (Formel) berechnen

Es gibt drei Gesetze zur gleichmäßig beschleunigten Bewegung. Diese Gesetze liefern Informationen zu Strecke, Beschleunigung, Zeit, Anfangsgeschwindigkeit  und Anfangsweg.

Formel gleichmäßig beschleunigte Bewegung ( Weg-Zeit-Gesetz ):

• s = 0,5 · a · t² + v_o · t + s₀
• "s" ist die Strecke in Meter [m]
• "a" ist die Beschleunigung in Meter pro Sekunde-Quadrat [m/s²]
• "t" ist die Zeit in Sekunden [s]
• "s₀" ist der Anfangsweg [m]

Beginnt die Bewegung aus dem Stillstand und vom Anfangspunkt aus, vereinfacht sich die Formel zu:  s = 0,5 · a · t²

Formel gleichmäßig beschleunigte Bewegung (Geschwindigkeit-Zeit-Gesetz):

• v = a · t + v₀
• "v" ist die Geschwindigkeit in Meter pro Sekunde [m/s]
• "a" ist die Beschleunigung in Meter pro Sekunde-Quadrat [ m/s² ]
• "t" ist die Zeit in Sekunden [s]
• "v₀" ist die Anfangsgeschwindigkeit in Meter pro Sekunde [ m/s ]

Beginnt die Bewegung ohne Startgeschwindigkeit, vereinfacht sich die Formel zu: v = a · t
Formel gleichmäßig beschleunigte Bewegung (Beschleunigung-Zeit-Gesetz):

• a = konstant
• "a" ist die Beschleunigung in Meter pro Sekunde-Quadrat  [m/s²]

Gleichmäßig beschleunigte Bewegung: Beispiele

Zeit das ein oder andere Beispiel zur gleichmäßig beschleunigten Bewegung zu rechnen.

Beispiel 1:

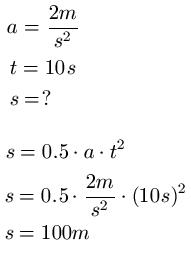
Beispiel 2:

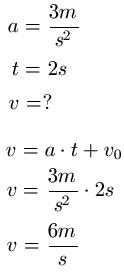
Umrechnung von Einheiten

Viele Schüler haben Probleme beim Umrechnen von Einheiten. Aus diesem Grund gehen wir hier noch einmal eine kurze Zusammenfassung der wichtigsten Umrechnungsregeln.

• 100cm = 1m = 0,001km
• 1m/s = 3,6km/h

Links:

• Übungen: Gleichmäßig beschleunigte Bewegung
• Zur Mechanik-Übersicht
• Zur Physik-Übersicht