Resultierende Kraft / Kräfte zerlegen

Mit der resultierenden Kraft und dem Zerlegen von Kräften befassen wir uns in diesem Artikel der Physik. Beides wird anhand von Beispielen erklärt. Dieser Artikel gehört zu unserem Bereich Mechanik.

In der Physik bzw. in der Mechanik geht es manchmal darum Kräfte zu zerlegen bzw. Kräfte zu einer resultierenden Kraft zusammen zu fassen. Mit beidem befassen wir uns in diesem Artikel. Dabei soll sowohl eine rechnerische als auch eine grafische Lösung für das jeweilige Problem angegeben werden. Für alle, die sich unter einer Kraft noch nichts vorstellen können, stehen noch die folgenden Inhalte bereit.

• Kräfte
• Newtonsche Gesetze
• Vektorrechnung ( Mathematik )

Zusammensetzen von Kräften / Resultierende Kraft

Wirken auf einen Körper an einer Stelle mehrere Kräfte, so kann man diese zu einer Kraft zusammenfassen. Man bezeichnet diese zusammengefasste Kraft dann als resultierende Kraft. Diese kann man sowohl grafisch als auch rechnerisch bestimmen. Beides soll nun gezeigt werden.

Kräfte in die gleiche Richtung:

Beginnen wir mit dem recht einfachen Fall, dass zwei Kräfte an einem Körper angreifen und diese in die gleiche Richtung wirken. In diesem Fall addieren sich beide Kräfte schlicht und ergreifend zu einer resultierenden Kraft. Die folgende Grafik zeigt dies:

Kräfte in entgegengesetzter Richtung:

Zwei Kräfte können auch in entgegengesetzter Richtung an einem Körper angreifen. Für diesen Fall werden die beiden Kräfte dann voneinander abgezogen. Auch hier wieder die allgemeine Darstellung als Grafik und die Formel samt einem Beispiel.

Kräfte unter einem Winkel:

Als nächstes sehen wir uns an, wenn zwei Kräfte unter einem Winkel gemeinsam an einem Punkt wirken. Auch hier wie immer die grafische und rechnerische Lösung. Bei der grafischen Lösung wird dabei ein Parallelogramm  gezeichnet. Dabei taucht für diesen Fall noch ein Winkel auf. Zwei Hinweise: Da dieser Artikel auch für Schüler der Mittelstufe einigermaßen verständlich sein soll, wurde bei der Gleichung auf die Vektorschreibweise verzichtet. Die Gleichung zur Berechnung der resultierenden Kraft bedient sich am Kosinussatz.

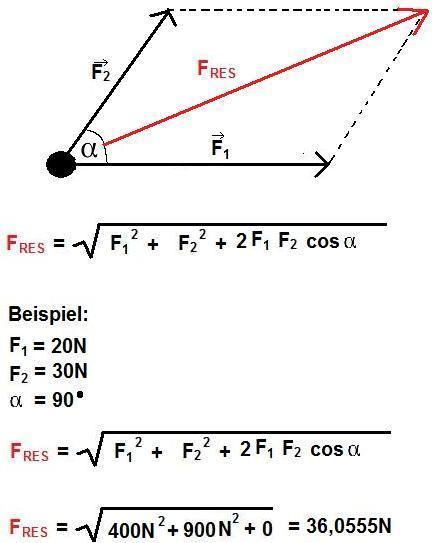
Hinweis:

Was passiert nun, wenn mehr als zwei Kräfte zusammengefasst werden müssen? In einem solchen Fall kann man erst zwei der Kräfte zusammenfassen und dann diese beiden zusammengefassten Kräfte mit der dritten zusammenfassen etc. Bis eine resultierende Kraft ermittelt wurde.

Kräfte zerlegen und Kräfteparallelogramm

Im letzten Abschnitt haben wir Kräfte zusammengefasst. Nun gehen wir den umgekehrten Weg: Wir zerlegen eine resultierende Kraft in zwei Einzelkräfte. Auch hier hilft das Kräfteparallelogramm. Wir sehen uns das ganze am Beispiel einer schiefen Ebene an.

Links:

• Zur Mechanik-Übersicht
• Zur Physik-Übersicht