Schiefe Ebene (Physik)

Die schiefe Ebene wird in diesem Kapitel ausführlich erklärt. Dabei zeigen wir euch die Formeln zur Berechnung von Geschwindigkeiten und Objekten an einem Hang. In diesem Zusammenhang tauchen auch Begriffe wir Hangabtriebskraft, Normalkomponente der Gewichtskraft und Reibung auf.

An einem Hang war jeder schon einmal. Entweder zu Fuß oder mit dem Auto. Da steht man auf einem Berg und es geht abwärts oder man möchte von unten auf einen Berg drauf fahren. Dies wird in der Physik mit einer schiefen Ebene beschrieben. Bevor wir jedoch anfangen, an dieser einige Berechnungen durchzuführen, sind einige Vorkenntnisse nötig. Wer mit den folgenden Themen noch Probleme hat, sollte diese nachlesen. Wer sich in den folgenden Themen hingegen grundlegend auskennt, der kann dies überspringen:

• Mathematik: Lineare Gleichungen
• Physik: Gleichmäßig beschleunigte Bewegung
• Physik: Kraft / Kräfte nach Isaac Newton

Schiefe Ebene: Formeln

In diesem Abschnitt liefern wir euch die Formeln zum Rechnen an der schiefen Ebene. Diese beziehen sich alle auf das folgende Bild. Schaut euch dieses erst einmal an, darunter gibt es noch einige Informationen.

Dies ist eine schiefe Ebene: Je größer die Steigung, desto größer ist der Winkel α. Hier noch ein paar Erklärungen zu den eingetragenen Kräften. Die Formeln folgen anschließend:

• Die Kraft F_G ist die Gewichtskraft des Körpers. Diese berechnet sich aus Masse mal Erdbeschleunigung für das Objekt. Die Einheit ist Newton.
• F_A ist die Hangabtriebskraft. Diese entspricht der Kraft, welche das Objekt nach unten rutschen lässt. Die Einheit ist Newton.
• F_GN die Normalkomponente der Gewichtskraft. Diese entspricht der Kraft, welche das Objekt auf den Berg drückt. Die Einheit ist Newton.

Es folgen nun die Formeln zu Berechnung der einzelnen Größen. Dazu gibt es noch Formeln, die Reibung mit einbezieht, die an der Oberfläche des Körpers herrscht und die Bewegung bremst. Sofern ein Reibwert in einer Aufgabe gegeben ist oder dieser berechnet werden soll, werden diese Formeln benötigt. Dabei unterschiedet man zwischen Haftreibung (wenn das Objekt noch stillsteht) und Gleitreibung (wenn das Objekt sich bewegt). Anmerkung: In der Realität gibt es immer Reibung. Manchmal ist sie jedoch so klein, dass man sie nicht mit einberechnet.

Gewichtskraft F_G berechnen:

• Formel: F_G = m · g
• "F_G" ist die Gewichtskraft in Newton [ N ]
• "m" ist die Masse in Kilogramm [ kg ]
• "g" ist die Erdbeschleunigung in Meter pro Sekunde-Quadrat [ m/s² ]

Hangabtriebskraft F_A berechnen:

• Formel: F_A = m · g · sin(α)
• "F_A" ist die Hangabtriebskraft in Newton [ N ]
• "m" ist die Masse des Körpers in Kilogramm [ kg ]
• "g" ist die Erdbeschleunigung in Meter pro Sekunde-Quadrat [ m/s² ]
• "α" ist der Winkel des Berges in Grad

Normalkomponente der Gewichtskraft F_GN berechnen:

• Formel: F_GN = m · g · cos(α)
• "F_GN" ist die Normalkomponente der Gewichtskraft in Newton [ N ]
• "m" ist die Masse in Kilogramm [ kg ]
• "g" ist die Erdbeschleunigung in Meter pro Sekunde-Quadrat [ m/s² ]
• "α" ist der Winkel des Berges in Grad

Haftreibung F_R' berechnen:

• Formel F_R' = μ' · F_GN
• "F_R'" ist die Haftreibungskraft in Newton [ N ]
• "μ'" ist die Haftreibungszahl und ist Einheitenlos
• "F_GN" ist die Normalkomponente der Gewichtskraft in Newton [ N ]

Gleitreibung F_R berechnen:

• Formel F_R = μ · F_GN
• "F_R" ist die Gleitreibungskraft in Newton [ N ]
• "μ" ist die Gleitreibungszahl und ist Einheitenlos
• "F_GN" ist die Normalkomponente der Gewichtskraft in Newton [ N ]

Schiefe Ebene Beispiele

Im nun Folgenden sehen wir uns Beispiele zur Rechnung an der schiefen Ebene an. Dabei werden wir auch Formeln aus der gleichförmig beschleunigten Bewegung und Kräfte benötigen.

Beispiel 1:

Eine 50kg schwere Kiste rutscht eine 20 Grad schiefe Ebene runter. Mit wecher Beschleunigung rutscht die Kiste - sofern reibungsfrei - die Ebene runter?

Lösung: Wir entnehmen dem Text die benötigen Informationen und berechnen damit die Hangabtriebskraft F_A. Mit dieser berechnen wir anschließend die Beschleunigung der Kiste. Hinweis: Kleine Unterschiede in der Berechnung hängen davon ab, wo und wie man rundet.

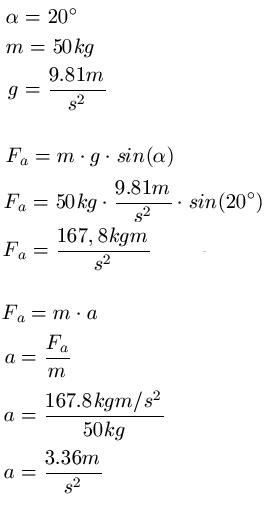
Beispiel 2:

Eine 50kg schwere Kiste rutscht eine 20 Grad schiefe Ebene runter. Die Gleitreibung soll mit μ = 0.03 berücksichtigt werden. Wie schnell ist die Kiste nach 50 Meter Strecke?

Lösung: Wir entnehmen dem Text zunächst alle relevanten Informationen. Anschließend berechnen wir die Hangabtriebskraft. Um nun noch die Reibungskraft zu berechnen, benötigen wir zunächst noch die Normalkomponente der Gewichtskraft. Hinweis: Kleine Unterschiede in der Berechnung hängen davon ab, wo und wie man rundet.

Wir haben nun die Hangabtriebskraft und die Reibungskraft berechnet. Diese wirken entgegengesetzt. Aus diesem Grund ziehen wir die beiden Kräfte voneinander ab. Anschließend berechnen wir die Beschleunigung, welche auf die Kiste wirkt. Über die Streckenformel erhalten wir dadurch die Zeit und können mit dieser auf die Geschwindigkeit schließen.

Links:

• Aufgaben: Schiefe Ebene
• Zur Mechanik-Übersicht
• Zur Physik-Übersicht