Aufleiten Flächenberechnung ( Aufleitung )

In diesem Artikel geht es um das Integral bzw. das Aufleiten. Zur besseren Übersicht sehen wir uns als erstes einmal an, was es mit der Aufleitung überhaupt auf sich hat. Und danach findet ihr Links um die verschiedenen Regeln zu erlernen.

Zunächst ein wichtiger Hinweis: Der Begriff "Aufleiten" ist umgangssprachlich. Er wird von vielen Schülern einfach als das Gegenteil von Ableiten angesehen. In der Mathematik spricht man bei diesem Bereich richtigerweise von Integration bzw. von Integrationsregeln. Dieser Artikel hier richtet sich also mehr an Schüler bzw. Studenten, die sich der Sache von der Umgangssprache her genähert haben.

Integral und aufleiten

Was soll das mit dem Integrieren bzw. Aufleiten überhaupt? Nun, es geht letztlich darum die Fläche unter einer Funktion zu berechnen. Um das zu verstehe, zeige ich euch im Folgenden, was es mit der Summenregel auf sich hat. Ziel ist es, die Fläche unter einer Funktion  zu berechnen. Wir beginnen dabei mit der Untersumme. Schaut euch einmal die folgende Grafik an:

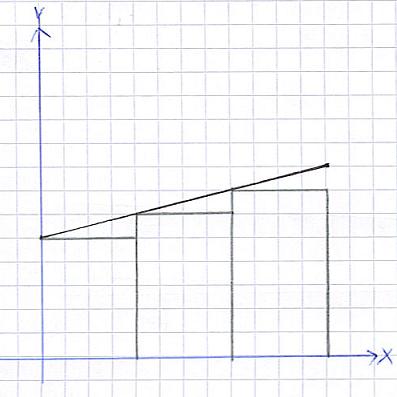
Die Untersumme: In schwarz wird die Funktion dargestellt. Um die Fläche unter dieser zu berechnen, wurden Rechtecke eingezeichnet ( Breite: 2cm ). Wir ihr sicher wisst: Die Fläche eines Rechtecks berechnet sich aus Länge mal Breite. Man kann somit die Fläche aller Rechtecke ausrechnen und zusammen addieren. So erhält man die Fläche unter einer Funktion. Allerdings entsteht hier ein kleiner Fehler: Wie ihr sehen könnt, fehlt ein kleines Stück Fläche zwischen den Rechtecken und der Funktion. Es "fehlt" also Fläche. Das war die Untersumme.

Die Obersumme: Als nächstes beschäftigen wir uns mit der Obersumme. Die Vorgehensweise ist sehr ähnlich zur Untersumme. Nur hier werden die Rechtecke etwas größer angesetzt. Werft aber erst einmal einen Blick auf die folgende Grafik:

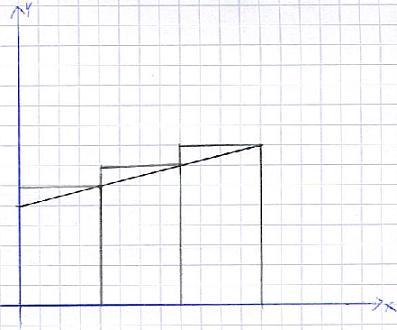
Es werden also erneut Rechtecke eingezeichnet. Deren Flächeninhalte berechnet sich wie immer aus Länge mal Breite. Und die einzelnen Rechtecke werden zu einer Gesamtsumme addiert. Nur hier ist die Summe größer als die eigentliche Fläche. Somit hat die Untersumme eine Fläche geliefert, die zu klein ist. Die Obersumme hingegen hat eine Fläche geliefert, die zu groß ist. Die richtige Lösung muss also irgendwo dazwischen liegen. Um die Integration zu vereinfachen, werden wir im nun Folgenden Regeln einsetzen um dies zu ermöglichen. Es folgt nun eine Liste der jeweiligen Regeln, sofern euch diese interessieren.

• Elementare Integrationsregeln
• Partielle Integration
• Fläche zwischen Funktionen
• Integration durch Substitution

Aufleiten und Flächenberechnung

Zeichnet man eine Funktion, so ergibt das oftmals einen sehr "langen" Verlauf. Jetzt will man natürlich nicht die komplette Fläche unter einer Funktion erhalten, die ist oftmals unendlich. Sondern nur die Fläche in einem gewissen Abschnitt. Deshalb setzt man so genannte Integrationsgrenzen. Schaut euch dazu erst einmal die folgende Grafik an:

Die Integrationsgrenzen werden meist mit a und b bezeichnet, wobei a die "untere" Integrationsgrenze und "b" die "obere" Integrationsgrenze bezeichnen. Heißt auf gut Deutsch: Die Fläche unter der Funktion von a bis b ist gesucht. Um diese zu bekommen müsst ihr wie folgt vorgehen:

• Integriert die Funktion mittels der Integrationsregeln
• Die Konstante "C" wird 0 gesetzt, sprich sie verschwindet
• Die Funktion mit oberer Grenze minus Funktion mit unterer Grenze berechnen

Beispiel 1:

Erklärungen: Die Funktion wird zunächst integriert. Die Stammfunktion wird in Klammern gesetzt und die Integrationsgrenzen werden an diese angetragen. Danach wird die Funktion ausgerechnet mit dem oberen Grenzwert: Setzt man die 1 in die Gleichung ein, erhält man ein Drittel. Danach wird ein minus "-" gesetzt". Hinter diesem wird der Funktionswert für die untere Grenze gebildet. Setzt man die 0 ein, ergibt sich eine Null. Dies ergibt ein Drittel als Gesamtergebnis.

• Weitere Beispiele zur Aufleitung Flächenberechnung

Links:

• Zur Integral-Übersicht
• Zur Mathematik-Übersicht