Quadratische Funktionen zeichnen und Parabeln

In diesem Abschnitt beschäftigen wir uns mit den so genannten quadratischen Funktionen und dem Zeichnen dieser. Dabei zeigen wir euch zunächst, worum es sich bei diesem Funktionstyp überhaupt handelt. Anschließend gehen wir auf das Zeichen dieser ein.

Als quadratische Funktion bezeichnet man eine Funktion, welche die folgende Form hat: f(x) = ax² + bx + c mit a ungleich Null. Oftmals wird auch die Gleichung y = ax² + bx + c verwendet. Dabei sind a, b und c beliebige Zahlen, wobei a wie bereits beschrieben ungleich Null sein muss. Die folgenden Beispiele demonstrieren dies:

• y = 5x² + 3x + 5
• y = 2x² + 2x + 8
• y = 4x² + 2
• y = 2x²

Quadratische Funktion: Parabel

Beginnen wir mit einer quadratischen Funktion, die besonders einfach ist: Einer Parabel. Diese hat zum Beispiel die Form f(x) = y = x² und soll im Folgenden gezeichnet werden. Für alle, die sich unter einer Wertetabelle oder einem Koordinatensystem noch nichts vorstellen können, steht der Artikel Lineare Funktionen bereit ( Wird in neuem Browser-Fenster geöffnet ).

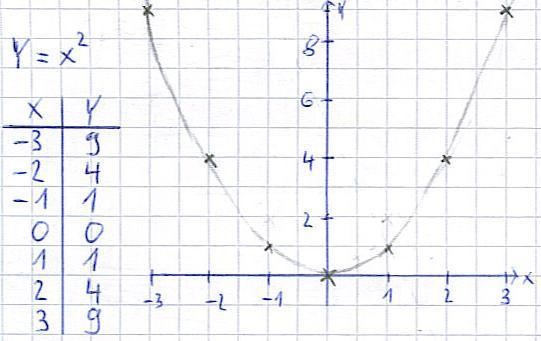
So werden quadratischen Funktionen und Parabeln gezeichnet:

• Zuerst die Wertetabelle anlegen. Dazu werden wie immer Zahlen für x eingesetzt und damit y ausgerechnet.
• An den Schnittstellen x-y die Kreuzchen machen um die Schnittpunkte zu markieren.
• Die Punkte werden verbunden. Wir haben hier jedoch keinen linearen Zusammenhang. Deswegen dürft ihr keine Gerade zeichnen, sondern den Verlauf in etwa "vorhersehen". Wer damit noch Probleme hat, der sollte nicht nur Zahlen wie 1, 2, 3 für x einsetzen, sondern auch Dezimalzahlen / Kommazahlen ( 1,2 oder 1,3 etc. ) um mehr Punkte zu finden.
• Die Funktion setzt sich natürlich weiter nach oben fort, auch wenn keine zusätzlichen Punkte eingetragen weden.

Quadratische Funktion: Beispiel 2

Die Parabel, die wir uns eben angesehen haben, war noch recht einfach. Zum besseren Verständnis, wollen wir nun eine etwas kompliziertere Funktion zeichnen. Dazu nehmen wir uns die Funktion f(x) = y = -0,5x² + 3 vor. Auch hier erstellen wir wieder eine Wertetabelle und zeichnen mit dieser die Funktion in ein x-y-Koordinatensystem ein.

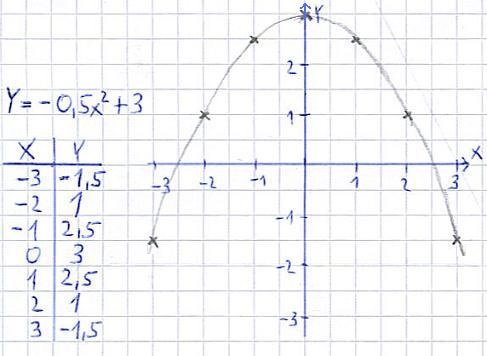
Hinweis: Von der Vorgehensweise ist es immer das selbe Spiel:  Wertetabelle, Punkte einzeichnen und Punkte verbinden. Das unangenehme bei dieser Funktion ist das Vorzeichen, wenn eine negative Zahl eingesetzt wird. Hier ein Beispiel für die erste Rechnung:

• y = -0,5 · (-3)² + 3 = -0,5 · 9 + 3 = -4,5 + 3 = -1,5.

Um fit im Zeichnen von quadratischen Funktionen zu werden, rate ich euch, unsere Übungen und Aufgaben zum Thema selbst durchzuführen.

Links:

• Weiter zu "Exponentialfunktion und E-Funktion"
• Zurück zur "Funktionen zeichnen Übersicht"
• Zurück zur Mathematik-Übersicht