Wichtige Eigenschaften und Formeln zu einem Rechteck lernst du hier. Du erfährst wie der Flächeninhalt und der Umfang von einem Rechteck berechnet werden und ob ein Rechteck ein Volumen hat. Die Inhalte liegen als Text und als Video vor.
Ein Rechteck ist ein Viereck mit speziellen Eigenschaften: Ein Rechteck hat 4 Seiten und 4 Ecken. Die gegenüberliegenden Seiten sind gleich lang und parallel. Es gibt 4 Innenwinkel mit jeweils 90 Grad. Die Seitenlängen werden meistens mit "a" und "b" bezeichnet.

Um das Rechteck zu beschriften werden die Eckpunkte mit den großen Buchstaben A, B, C und D beschriftet. Dies erfolgt gegen den Uhrzeigersinn. Die Seiten werden mit "a" und "b" bezeichnet. Die beiden Diagonalen gehen von einer Ecke in die gegenüberliegende Ecke und werden mit "d" bezeichnet.

Hinweis: Um die Grafik nicht zu unübersichtlich zu machen wurde im vorigen Rechteck nur eine Diagonale eingezeichnet.
Rechteck Eigenschaften und Formeln
Dies sind die wichtigsten Eigenschaften eines Rechtecks:
- Es ist ein Viereck mit - wie der Name sagt - 4 Ecken.
- Es gibt 4 Seiten.
- Die gegenüberliegenden Seiten sind gleich lang.
- Die gegenüberliegenden Seiten sind parallel.
- Alle Winkel sind 90 Grad groß (rechter Winkel).
- Die Summe der Innenwinkel beträgt 360 Grad.
- Beide Diagonale sind gleich lang und halbieren einander.
Aufbau eines Rechtecks:
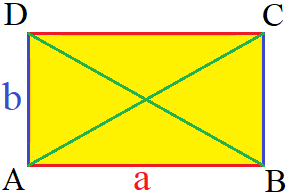
Die wichtigsten Formeln zum Rechteck dienen dazu mit den Seitenlängen "a" und "b" den Flächeninhalt "A", den Umfang "U" und die Diagonalen "d" zu berechnen. Ergänzend noch die Formel zum Umkreisradius "ru".
Formeln Rechteck:

Beispiele zu den Formeln folgen weiter unten.
Unterschied Rechteck, Quadrat und Vierecke
Ein Rechteck ist ein Viereck. Jedoch könnten Vierecke ganz anders aussehen als ein Rechteck. Die nächste Grafik zeigt ein Viereck, welches jedoch keinen rechten Winkel aufweist und keine parallelen Seiten hat.
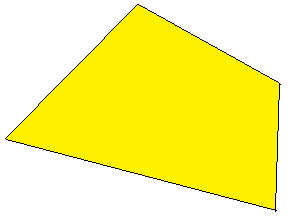
Ein besonderes Rechteck ist das Quadrat. Ein Quadrat hat ist ebenfalls ein Viereck, jedoch mit 4 gleich langen Seiten. Daher werden alle Seiten mit einem "a" bezeichnet und nicht wie bei einem Rechteck mit "a" und "b".
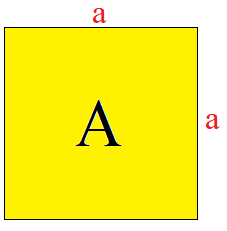
Die Formeln zur Berechnung des Rechtecks funktionieren auch beim Quadrat. Da jedoch Länge und Breite des Quadrats gleich sind (a = b) können die Formeln für das Quadrat für Flächeninhalt und Umfang vereinfacht werden.

Mehr zu diesem Thema erfährst du unter Quadrat.
Rechteck Flächeninhalt: Die Fläche berechnen
Der Flächeninhalt eines Rechtecks gibt an, wie groß das Rechteck ist. Die gelbe Fläche in der nächsten Grafik zeigt was mit dem Flächeninhalt gemeint ist. In Formeln wird der Flächeninhalt mit "A" bezeichnet.

Die Fläche bekommst du durch Multiplikation der Länge mit der Breite.
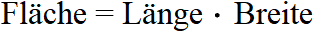
Als Beispiel für die Formel und die Berechnung der Fläche dient ein Rechteck mit den Seitenlängen 4 Meter und 3 Meter.

Die Formel zur Berechnung des Flächeninhaltes "A" sieht vor die Seitenlängen mit a = 4 m und b = 3 m miteinander zu multiplizieren.

Ein Rechteck mit 4 m auf 3 m Seitenlängen hat eine Fläche von 12 Quadratmeter. Mehr zu diesem Thema lernst du unter Rechteck Flächeninhalt berechnen.
Umfang des Rechtecks berechnen
Der Umfang des Rechtecks gibt an, wie lange der Rand des Rechtecks ist. Dieser entspricht der Strecke um einmal am Rande des Rechtecks herum zu laufen. Mathematisch ist es die Länge aller Seiten aufaddiert. Der Umfang wird in Formeln mit "U" bezeichnet und lässt sich mit der folgenden Gleichung berechnen.

Als Beispiel haben wir ein Rechteck mit den Seitenlängen a = 30 cm und b = 20 cm. Wie groß ist der Umfang?

Zur Lösung der Aufgabe setzen wir a = 30 cm und b = 20 cm in die Formel ein. Beachte bei der Berechnung die Regel Punkt vor Strich. Dies bedeutet, dass zuerst die Multiplikationen berechnet werden müssen und danach die Addition.

Ein Rechteck mit den Seitenlängen 30 cm und 20 cm hat einen Umfang von 100 cm. Weitere Erklärungen und Beispiele zu diesem Thema findest du unter Rechteck Umfang berechnen.
Seitenlängen: Länge und Breite berechnen
Mit den Formeln zum Rechteck lassen sich die Seitenlängen "a" und "b" berechnen. Dazu wird die Formel zum Flächeninhalt "A" nach einer der beiden Seitenlängen umgestellt. Mit diesen Formeln lässt sich Länge oder Breite eines Rechtecks berechnen.
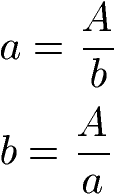
Als Beispiel sei der Flächeninhalt eines Rechtecks mit 20 Quadratmeter und die Seitenlänge "a" mit 5 Meter gegeben. Mit diesen Angaben soll die Seitenlänge "b" berechnet werden.
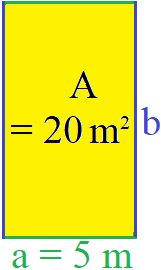
Da wir b berechnen wollen, verwenden wir die Formel bzw. Gleichung welche nach "b" aufgelöst ist. Wir setzen A = 20 m2 ein sowie a = 5 m. Die Berechnung liefert 20 : 5 = 4. Meter kürzt sich raus.

Die Seitenlänge "b" ist 4 Meter lang.
Rechteck Diagonale berechnen
Die Diagonale geht vor einer Ecke in die gegenüberliegende Ecke. Um die Diagonale eines Rechtecks zu berechnen wird die Formel zum Satz des Pythagoras verwendet.
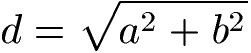
Als Beispiel liegen die Seitenlängen 8 m und 5 m vor. Die Diagonale des Rechtecks soll berechnet werden.
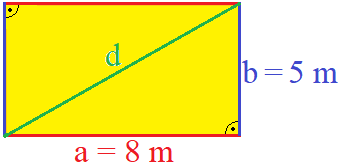
Die Längen der Seiten setzen wir mit a = 8 m und b = 5 m in die Formel zur Diagonale ein. Wir quadrieren beide Angaben unter der Wurzel und fassen diese zusammen. Die Wurzel wird gezogen und ergibt eine Diagonale von etwa 9,433 Meter Länge.

Wichtig: Beim Quadrieren und Wurzel ziehen werden sowohl die Zahlen als auch die Einheiten berücksichtigt. Daher wird beim Quadrieren aus m nun m2 oder beim Ziehen der Wurzel aus m2 wieder m.
Volumen eines Rechtecks oder Quaders berechnen
Ein Rechteck ist eine Ebene Fläche und besitzt keine Höhe.

Da ein Rechteck keine Höhe besitzt, gibt es auch kein Volumen. Das Volumen eines Rechtecks ist Null.
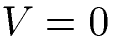
Sprechen Personen vom Volumen eines Rechtecks meinen sie dabei meistens einen Quader. Ein Quader wird aus 6 Rechtecken zusammengesetzt.
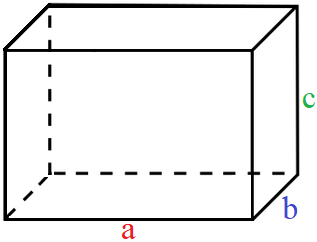
Ein Quader ist im Gegensatz zu einem Rechteck ein räumliches Gebilde mit Länge, Breite und Höhe. Das Volumen ist die Multiplikation dieser drei Angaben. Da sich die Oberfläche eines Quaders aus Rechtecken bilden kann steckt in der Formel zum Volumen des Quaders die Fläche eines Rechtecks. Jedes Rechteck kommt 2 Mal vor und berechnet sich jeweils aus Länge mal Breite.
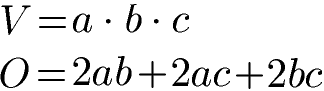
366 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige: